Chapter 6
INTERACTIVE RHYTHM LEARNING FOR PERCUSSION ROBOTS
The previous chapter introduced a method that allows a robot to learn how to produce particular timbres by example. How is the robot to know in what contexts these timbres should be used? Given a method of transcribing timbre from a human performance, as presented in Chapter 4, a robot might build a statistical model of when particular timbres are used, and incorporate that model into its own playing. This chapter shall present such a model. This shall be operationalized as the problem of learning rhythms, where a rhythm comprises a sequence of discrete timbral categories.
It is easy to make musical machines play fixed, static rhythms by, for instance, giving them MIDI files to play. There are also a number of techniques for generating rhythms according to some closed process (to be discussed in detail anon). However, the present goal is to make the robot listen to the human's playing and respond in a natural way. In particular, the goal is to make the robot capable of learning specific repeated rhythmic patterns, recall them according to context, and learn signal rhythms that trigger changes in the rhythmic patterns. In the absence of repeated rhythms, e.g. when the human is freely improvising, the goal is for the robot to learn the general character of the human's playing and generally match those features while sometimes introducing new but stylistically appropriate musical ideas.
6.1 Previous Work
This challenge intersects with several disciplines and there are several histories that converge upon it. There exists relevant work in the fields of algorithmic composition, interactive computer music, musical robots, and statistical machine learning, yet none of these alone provides a complete approach. The following sections shall construct a variety of histories that together provide a starting point for the question at hand.
6.1.1 Algorithmic Composition
In a certain sense, this question falls within domain of algorithmic composition, insofar as the goal is to write a procedure that generates music for a robot to play. There are many algorithms that have been used to aide composition since well before digital computers. One common algorithm's objective is to maintain a particular statistical distribution amongst elements in the composition. For example, at the beginning of the 20th century, works such as Joseph Hauer's 1909 composition Nomos [76], his theoretical treatise Sphaerenmusic [77], Arnold Schoenberg's Op. 23 [78], and Charles Ives 1901 composition From the Steeples and the Mountains [79] developed pitch-selection procedures that ensured a statical equivalence amongst the pitch classes. These techniques became popular, and in the following decades increasingly sophisticated musical machinery (function generators → analog synthesizers → digital computers) allowed composers such as Stockhausen and Milton Babbitt to apply these methods more rigorously to more aspects of music, including rhythm. Although interest in the style associated with this music (serialism) eventually waned, the idea of generating music by manipulating statistical distributions continued both in the creation of new musical styles [80] [81], and in the understanding of previous styles [82] [83].
Another popular algorithm involves choosing musical elements randomly from a set of options. An early example of this is found in Athanasius Kircher's 1650 treatise [28] where, under the heading `MUSURGIA MECHANICA', in Tomus II Lib VIII pars V, he describes the arca musarithmia, which allows laypeople to compose by piecing together randomly selected fragments of melodies, rhythms, and modes, drawn from box according to the poetic meter of the text to be set. One hundred and seven years later, C.P.E. Bach, evidently unaware of Kircher, wrote a short treatise entitled `Invention by which six measures of double counterpoint can be written without a knowledge of the rules', translated in [84]. This is essentially a two voice, six-bar composition in which each (empty) bar can be populated arbitrarily with one of 9 options for the descant and another 9 options for the bass (all composed by Bach). Similar compositions have been attributed to Hayden [85] (composed by M. Stadler according to the New Grove) and Mozart [86]. These pieces both have 16 bars and 11 options per bar - voices are not chosen separately - and a pair of dice are used to select from amongst these. In principle, the number of permutations that could be created using such a method quickly becomes astronomically high - i.e. nm, where n is the number of options per bar and m is the number of bars. However, in another sense, these 18th century examples are actually single compositions, as the options for each bar are simple variants of one another, and the underlying harmony and structural organization will be identical in all permutations. This history might continue through John Cage's use of indeterminacy, through David Cope's Emmy algorithm, which composes by recombining bits and pieces from existing works using sophisticated rules [87] [88], to any musician who has used a random or pseudo-random number generator in a computer program. However, as general histories of this nature meet digital computers, they typically become entangled in cybernetics and classic `hard AI' problems, where the goal increasingly becomes for a computer to write music with absolutely no human intervention.
By contrast, human intervention is the primary goal of this chapter. In particular, the goal is an interactive algorithm that takes a human's rhythm as input and generates an accompanying rhythm as output. Historically, the question of how to do this with pitches has been studied much more deeply than how to do so with rhythm. Indeed, attempts to proceduralize the melodic aspect of composition vastly predate digital computers. Music theory treatises from as far back as the 11th century show, given one melody, how to generate one or several new melodies to accompany the first, following a few simple rules [89]. This line of thought was greatly expanded in the 16th century, and it became common for music theorists to give lists of constraints (i.e. compositional `rules') that should be met when generating a new melody to accompany a given melody [90] [91][92]. For any given melody, there are typically only a small set of new melodies that will either meet the constraints or minimize the constraints that are broken. The advent of computers in the 20th century brought many attempts to mechanize these rules. Important pioneers were Lejaren Hiller and Leonard Isaacson whose work in the 1950's included experimentation with generating counterpoint in this style using the Illiac computer at University of Illinois at Urbana [93]. The work of Hiller and Isaacson culminated in the Illiac Suite, for string quartet, in which notes were generated and selected according to a variety of procedures (different in each movement). The result is often regarded as the first piece of music composed by a machine, and was transcribed for performance by human musicians [94]. Another seminal study at MIT showed that it is possible to generate counterpoint using second-order Markov chains [95]. Such a network can also learn the relative weights of the constraints by analyzing existing music. There are a few problems with this approach that limit its applicability in the current study. First, the constraints define a musical style, and are hard-coded into these systems, but the goal here is to learn the style rather than impose it. Furthermore, as this method became increasingly codified, rhythm was systematically removed from the model to the extent that later treatises on the subject proceed under the assumption that all notes that make up a melody are equal in duration [96], which was never the case in actual music of this style. Another problem is that these algorithms run offline and assume a time-flattened representation of music and are generally not suitable for realtime operation (including the ones that run sequentially).
6.1.2 Interactive Computer Music
Of course, this does not mean that no realtime, interactive music generation systems have been built. Robert Rowe's seminal system `Cypher' [97] implements several algorithms for generating musical gestures (in the form of MIDI), as well as many methods of systematically transforming those gestures. `Cypher' also analyzes MIDI data from a human player (and feedback from its own output), and extracts and classifies features from the local timescale of individual notes, and from the larger timescale of musical phrases. Users may then specify mappings between the analysis and synthesis. For instance, input notes classified as having `low' pitch could cause staccato output, or the amount of harmonic irregularity in input phrases could control phrase-length at the output. George Lewis's system `Voyager' [98] has a similar organization. It comprises a number of music generation algorithms that continually generate 64 streams of music, of which only a small ensemble are heard at at time. Every few seconds, a procedure selects a new ensemble and a new synthesis algorithm, as well as new synthesis parameters such as which scale, tempo, and timbre to use. `Voyager' also listens to up to two streams of MIDI input (or live input coupled to the system through a pitch follower that generates MIDI), and calculates features such as average pitch, velocity and note-spacing. The music generation algorithm can be set to imitate, oppose, or ignore features coming from either of the input streams. Although both systems have methods of dealing with musical time, neither deal explicitly with rhythm as a gestalt. In Joel Chadabe's interactive piece `Rhythms' [99], six musical voices loop subsequences of a larger, randomly determined rhythm, each voice maintaining a single pitch, while two additional voices play `melodies' by looping subsequences of a larger sequence of pitches. A human triggers changes in the music (length and starting position of the subsequences) by pressing keys on a computer keyboard, although the nature of the changes are randomly determined. In all of the foregoing interactive systems, the behaviour is either hard-coded, or is manually configured by the user; none learn their behavior by listening.
6.1.3 Musical Robots
In a few instances, interactive algorithmic musical systems have even been implemented in robotic percussion players. Weinberg and Driscoll's composition Pow uses a call-and-response paradigm to generate rhythms [47]. In one part of this composition, a human plays a rhythm, and the robot responds by selecting a rhythm from a large database of constructed rhythms (made by exhaustively subdividing beats in different ways). The robot's selection is made according to two user-defined parameters - similarity and stability. The similarity measure indicates how similar the robot's response should be to the human's call, and stability indicates how chaotic-sounding the robot's response should be, which is operationalized using the notion of rhythmic expectancy defined in [100]. In their robotic Marimba player, Hoffman and Weinberg focus on generating jazz accompaniment in a way that is inspired by the notion of physical gesture rather than note sequences [8]. One simple way that they achieve this is to have the four arms move back and forth across the instrument (they are mounted on tracks) roughly in time with the music. Rhythmic patterns are preprogrammed, and if an arm happens by serendipity to be at the location of a note in the current chord at the moment it is supposed to play, then it will strike that note. In another mode of interaction the robot plays rhythms that are inspired by the human's rhythms. In this mode, the robot quantizes the human's rhythm and stores a decaying histogram representing the probability with which the human plays an onset in each quantization bin. In fact, it does this separately for each arm via clustering of the human's pitches. At every chord change, the arms are positioned above notes in the current chord. They then play a rhythm based on the probabilities in the histograms. Ajay Kapur's MahaDeviBot accompanies an augmented sitar by looking up rhythms in a database [48]. The database is populated with rhythms via automatic transcription recorded music. The sitar is fitted with a pressure sensor under the player's right thumb (whose position remains fixed against the neck while playing), and the signal from that sensor serves as the database keys. The sitar player initially generates keys by playing along with each rhythm in the database and recording thumb pressure. Then, during performance, the sitar player's thumb pressure is correlated with the keys in the database, and the drum robot plays the rhythm corresponding to the nearest matching key.
6.1.4 Machine Learning
In another sense, learning rhythmic timbral sequences can be viewed as a problem of pattern-recognition and sequence generation. Recent advances in training algorithms for neural networks have made them incredibly powerful tools for modeling sequences with long-term dependencies. A common task is to learn language one character at a time. In this model, the network's inputs encode the current character in the sequence, and the outputs represent the next character. At each step, the output is fed back into the input to generate the next character. One powerful technique for this task is the Long-Short-Term-Memory (LSTM) network [101]. One such study uses an LSTM to learn the first 100 megabytes of the English Wikipedia [102]. After training, it can generate new articles with valid markup including balanced xml tags, appropriate section headings, and (rather nonsensical) English text with locally correct grammar and a preponderance of words pertaining to a particular subject. Another technique is a standard Recurrent Neural Network (RNN) trained using Hessian Free (HF) Optimization [103]. In one study, this method was used to learn, amongst other things, the first 100 megabytes of text (without markup) from the English Wikipedia [104], again one character at a time. Although the results on this task are subjective, this technique has been shown to significantly outperform LSTM networks on standard sequence modeling tasks [105], and the results here appear to be at least similar. Another study uses a LSTM network to learn handwriting from pen-traces (sequences of (x, y) pen locations)[102]. The network's inputs encode the current pen location and its outputs encode a probability distribution for the subsequent pen location. Again, sequences are generated by feeding the output back into the input at each cycle. After training, this network can generate random lines of plausible-looking handwriting with, mostly valid characters, some valid words, and word breaks at plausible intervals, in a coherent, random, writing style. With some modifications it can be primed to generate handwriting mimicking a particular writer's style, indicating that it `remembers' subtle stylistic dependencies over the hundreds of pen coordinates that make up a line of text. Repeated characters are stylistically similar but not identical. If the concept of text is replaced with music, and characters with notes, the applicability of these studies to the current study should be clear, as music may also be seen as a sequence of notes with long-term structural and stylistic dependencies. Not surprisingly, these techniques have been applied to music generation. Here the focus shall be, perhaps somewhat unfairly, on the rhythmic approaches in those studies. One seminal study [106] uses an RNN to generate monophonic melodies. This study divides musical time into timepoints one eighth-note (quaver) in duration (definitions of `timepoints' and other representations of rhythm are given in Section 6.2.2 anon). At each timepoint, the rhythm is represented using two binary neurons - one to indicate whether a note is sounding at that timepoint, and another to indicate (given a repeated pitch) whether it is tied to the note in the previous timepoint. This network is trained using a variant of Back-Propagation Through Time (BPTT), and produces valid but relatively uninteresting melodies with simple rhythms. Another seminal study [107] extends the previous one in a number of ways. This system represents time as note durations, quantized to the nearest twelfth of a beat. Each duration is encoded with three values: the base 2 logarithm of the duration, the number of twelfths in the duration mod 3, and the number of twelfths mod 4. The latter two values are supposed to be rhythmic analogues to pitch chroma, and are each encoded as (x, y) coordinates on a circle to facilitate distance calculations. The author of that study reasons that encoding each note as a single duration rather than many timepoints helps the network learn long-term dependencies by greatly reducing the number of time-steps in a passage of music. Like the previous study, this algorithm generates music that is locally valid but mostly lacks higher-order structure. Both studies predate LSTM and HF optimization. Another similar study [108] uses a LSTM network to learn 12-bar blues. Rhythm is represented with timepoints, as above, but the end of a note is signaled by using a finer grid-spacing than necessary, and forcing the note ending to be marked with a zero. This study uses 2 timepoints per beat, effectively encoding quarter notes (crotchets), for a total of 96 timepoints in one 12-bar piece. The authors claim that the network learns global structure, but this is difficult to assess due to limitations in the training data. More recently, emerging RNN techniques have been applied to polyphonic transcription of audio signals and the analysis and generation of symbolic polyphonic music [109]. All these studies use training data with very simple rhythmic structure, and to the author's best knowledge, there has been no previous attempt to model more complicated functions of rhythm that are particular to percussion instruments using these techniques. Note again that these models operate without human interaction during composition, and therefore do not perfectly model the present goals.
6.2 Rhythmic Models
6.2.1 Components of Rhythm
A performed rhythm comprises at least three distinct temporal components: the structural component, tempo, and timing [110]. The structural component is the sequence of relative durations and metric positions indicated in a musical score, and is not typically altered by performers. Tempo is the overall speed at which the structural rhythm is played, which may include accelerandi and rallentandi marked in a score, as well as momentary, improvised fluctuations in speed used by the performer as an expressive device [110]. Timing is the relative lateness or earliness of individual notes as compared to the structural rhythm after tempo has been applied. Timing may be the result of noise in the human motor control system, or deliberate expressive decisions made by the performer [111] [112] [113] [114], and is not directly notated in musical scores. This study limits the model to include only the structural component of rhythm so it may be invariant to discrepancies in performance. The structural rhythm may be extracted from a performed rhythm by using tempo tracking to isolate tempo [115] [116] [117] [118] [73] [119] [120] [121] [122] [123] [124] [125] [126] [127] [128] [129], and quantization to isolate timing [100][130][131]. Those methods that are inherently predictive [117] [130] [119] [122] may be well-suited to the present purpose. There are also methods of doing the inverse: generating performances by applying tempo and timing to structural rhythm [111]. The word `rhythm' shall be used to refer to structural rhythm henceforth.
6.2.2 Representations of Rhythm
In order to proceduralize rhythm, it is necessary to find a suitable mathematical representation of rhythm. In the 1940s and '50s, the composer Milton Babbitt developed two such representations of rhythm. The first is known as a `duration series', and the second as a `timepoint series' [132]. Both deal only with note onsets. This limits them to monophonic rhythms, but does not preclude the use of rests, which can be conceptualized as having silent onsets. A duration series is an ordered set of integers representing relative durations. It is constructed by dividing an ordered set of inter-onset intervals by its greatest common divisor ∆τ. A timepoint series is an ordered set of integers representing the metric positions of note onsets. Suppose a grid is imposed on musical time, where the grid-spacing is ∆τ, and the grid positions are i ∆τ ∀ i ∈ ℕ. Timepoints are the indices 1 + (i\mod C), where C is the number of timepoints in a larger structural unit such as a beat or measure, and a timepoint series is the ordered set of those timepoints that are populated by onsets. These representations are depicted in Figure 23.
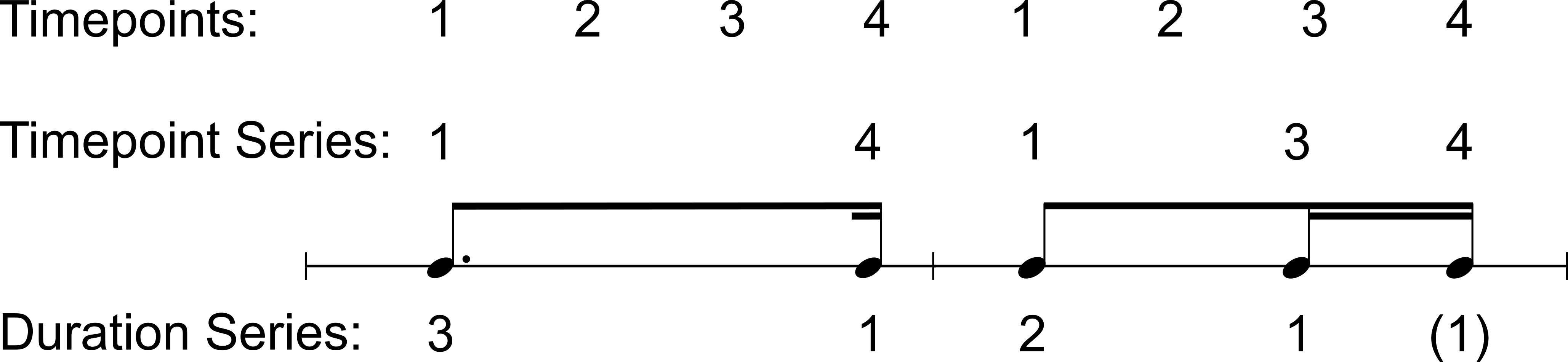
In theory, these representations are interchangeable, since, for i > 0, the ith member in timepoint series 𝕋 can be calculated as 𝕋i = (𝕋0+∑j=0i−1𝔻j)\mod C, where 𝔻j is the jth member of the duration series. However, in practice, if durations are obtained from a human performance through a noisy measurement and quantization process, the durations will most likely drift relative to the timepoints over time, and it is not safe to assume that a conversion can be made correctly. For example, consider the case in which a human plays a sequence of perceptually equal durations, and the observed (slightly unequal) durations are quantized (i.e. made equal) with a relaxation network such as [100][133], which operates directly on a list of observed durations. There is no guarantee that the sum of the durations will remain unaltered; the quantizer could marginally shorten all of the observed durations. If the result were converted to a timepoint representation by summing the durations and comparing this to a constant grid whose positions are calculated from the observed onset times, then the timepoints will be found to drift increasingly earlier with respect to the grid. Each representation has advantages and disadvantages. Babbitt eventually argued against the use of durational series on grounds that are mainly pertinent to his own compositional style [132]. For the case at hand, duration series have the advantage that they are amenable to sophisticated quantization methods such as connectionist methods [100], whereas timepoint series are most amenable to grid-based quantizers which typically do not perform as well. Additionally, an observed set of onset times may be encoded as a duration series with no knowledge of the tempo or the phase of the rhythm relative to the musical beat; this is desirable because extracting these from a performance can be messy. On the other hand, if a model is to operate in realtime, it will take small chunks of input and generate small chunks of output, and the input and output will have to remain in phase with each other. It is not possible to guarantee this with a durational representation of rhythm. Suppose, for instance, that the model is given small durations as inputs, and it continually outputs large durations. Over time the temporal separation between the input rhythm and output rhythm will be unbounded. Timepoints do not suffer this flaw as long durations can be built up in small chunks by repeated concatenations of ∅. This last problem does not seem tractable, and in any real system employing this algorithm, the tempo and phase of the rhythm relative to the beat will most likely have to be inferred for other reasons, so timepoints are probably the better representation for the current application.
6.3 Implementation
The following subsections shall first describe a basic, oversimplified model for learning rhythms, and in the subsequent subsections this basic model shall be expanded to make it suitable for real-world applications.
6.3.1 Basic Approach
6.3.1.1 Prediction
Let the assumption be made that the beat period and phase of the music are known, which can be achieved either by imposing these on the user (i.e. the robot determines these values and the human follows them), or by performing beat-tracking. Let it also be assumed that the human's onset times have been properly captured using onset detection or other means. Let it further be assumed that human either performs with metronomic precision, or that their playing has been properly quantized. The initial method presented here deals with one beat of music at a time, so C is set to the number of timepoints in a beat. Every beat of the input rhythm 𝕀 and output rhythm 𝕆 is encoded as a set of C real numbers. The values in 𝕀 indicate the certainty that the human played an onset at the respective timepoint; because perfect transcription is assumed, the input values used in this study will either be 0 or 1. The values in 𝕆 represent the probability that the robot will play an onset at the corresponding timepoint. At a time mathematically indistinguishable from the beginning of each beat (i.e. slightly before the beat, to account for computation time) 𝕀 in the previous beat is used to calculate 𝕆 in the subsequent beat. The model used is a feedforward neural network with C real-valued inputs and outputs (other architectures shall be discussed below). So, at the beginning of each beat, the network's inputs are loaded with 𝕀 and propagated through the network. The outputs are interpreted as 𝕆. This is depicted in Figure 24.
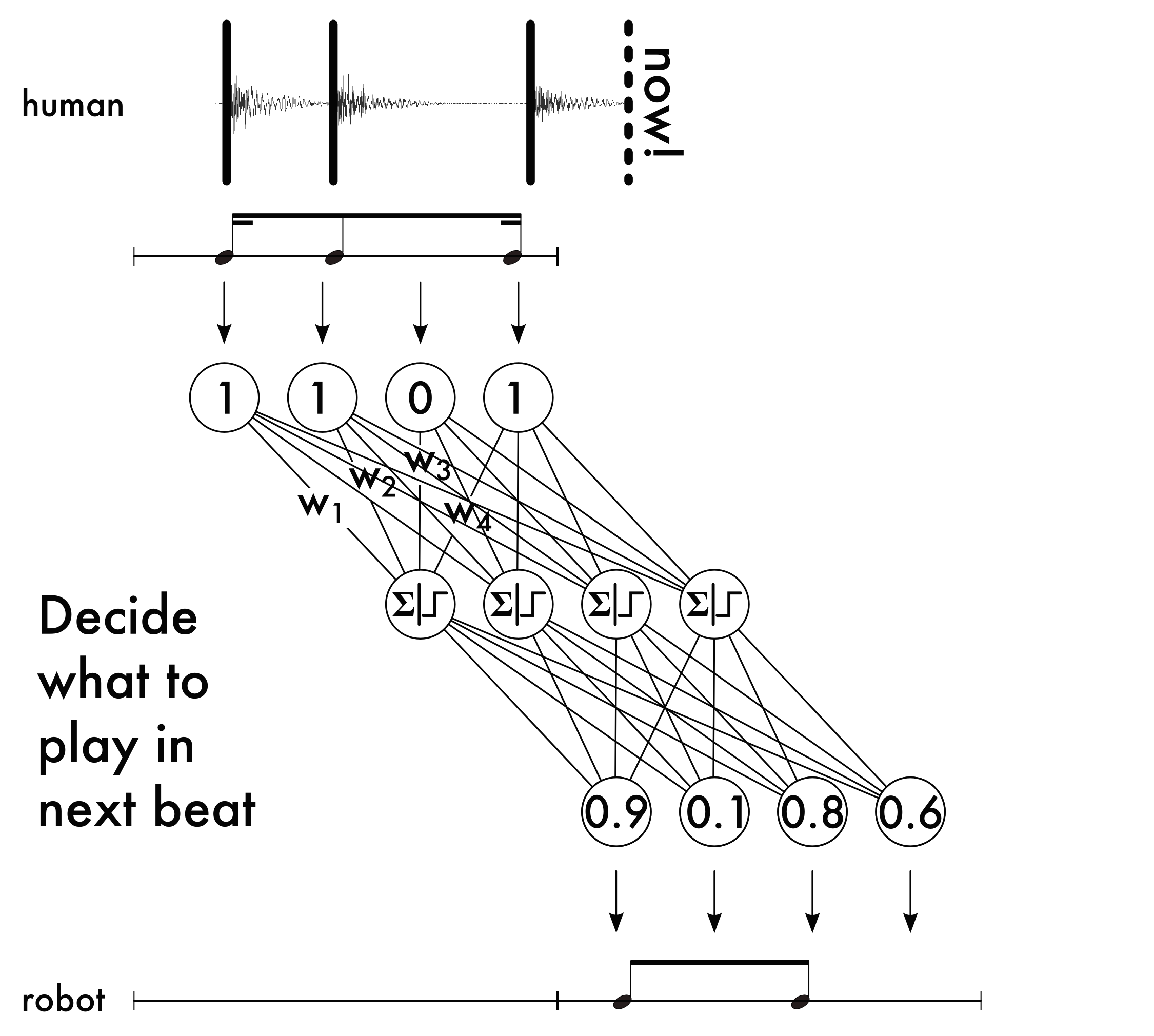
6.3.1.2 Learning
The network weights are initialized to random values. Consequently the outputs are random, so the network must be trained in order to produce meaningful output. It is desirable for the robot to be adaptable to musical characters that may be different between users or from moment to moment during interaction with a single user. For this reason an online learning strategy is adopted. It is possible to train a large network offline on a very large corpus of existing or constructed rhythms of different characters, thereby mimicking adaptability by brute force (this is further considered below). There may be certain advantages to this approach. However, an online approach is taken here for the following reasons.
- It is a design principal of interactive robots that they should treat humans as individuals, not just generic humans [134]. One way of achieving this is allowing the robot to learn different models for different humans.
- The author considers it to be a more poetically beautiful concept for the robot to learn directly from its interactors, and recall this information during subsequent interactions. This arrangement gives the robot a kind of personal history and also allows individuals to interact with each other through the robot, and such would not be the case with a strictly offline approach.
Online learning is accomplished by interpreting 𝕆 as a prediction about what 𝕀 will contain in the next beat (i.e. what the human will play). After making such a prediction at the beginning of one beat, the robot waits until the end of that beat to find out what 𝕀 actually contained. That rhythm is loaded into the network outputs, and the network weights are updated using the standard backpropagation / gradient descent algorithm, which attempts to nudge the network's weights towards values that would have caused the desired output for the given input. This is depicted in Figure 25.
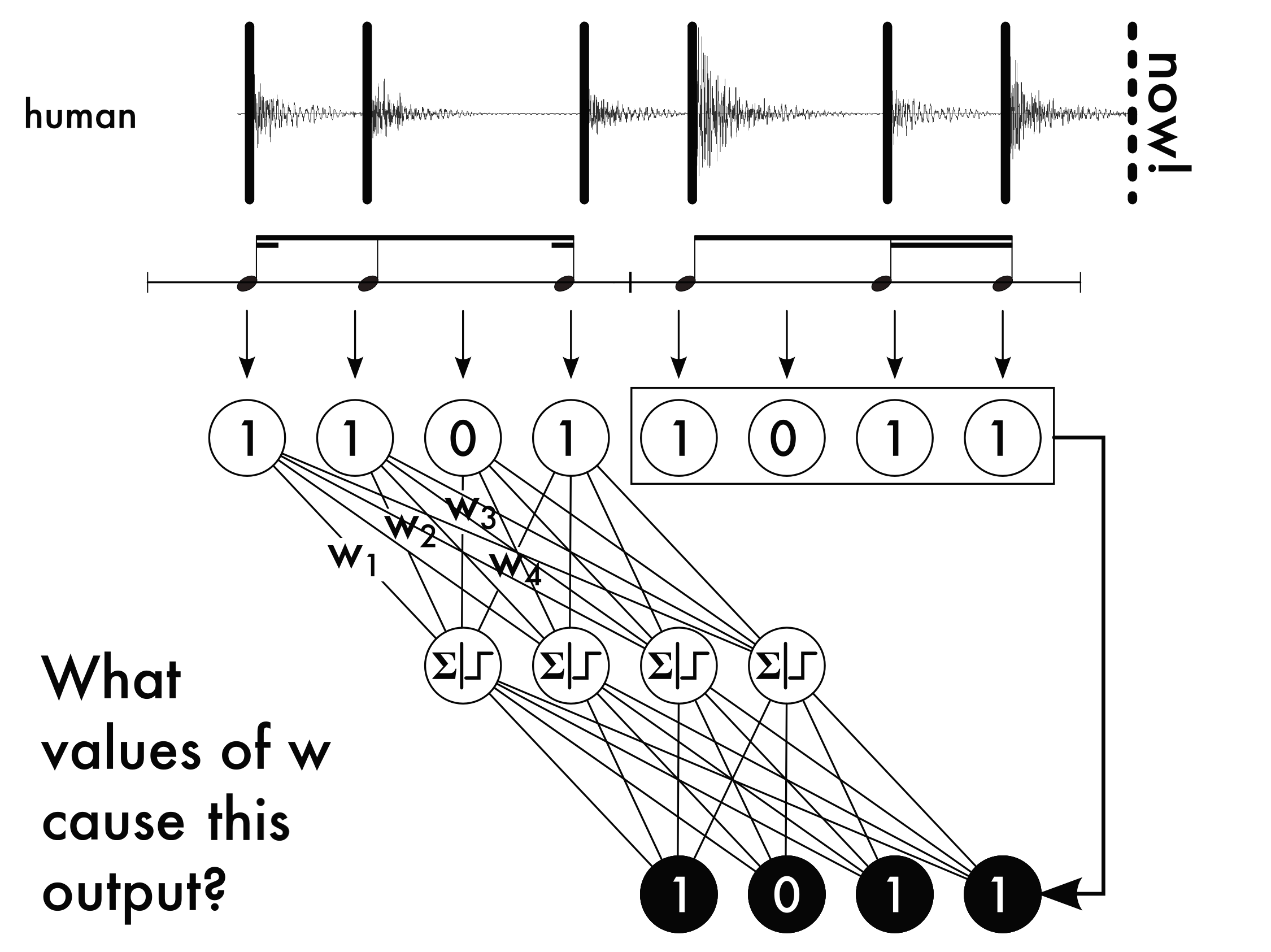
6.3.2 Improvements
The basic model as presented is capable of interactively generating timepoint series. However, it makes a number of assumptions that limit its applicability to the intended purpose. These shall be rectified presently.
6.3.2.1 Timbre
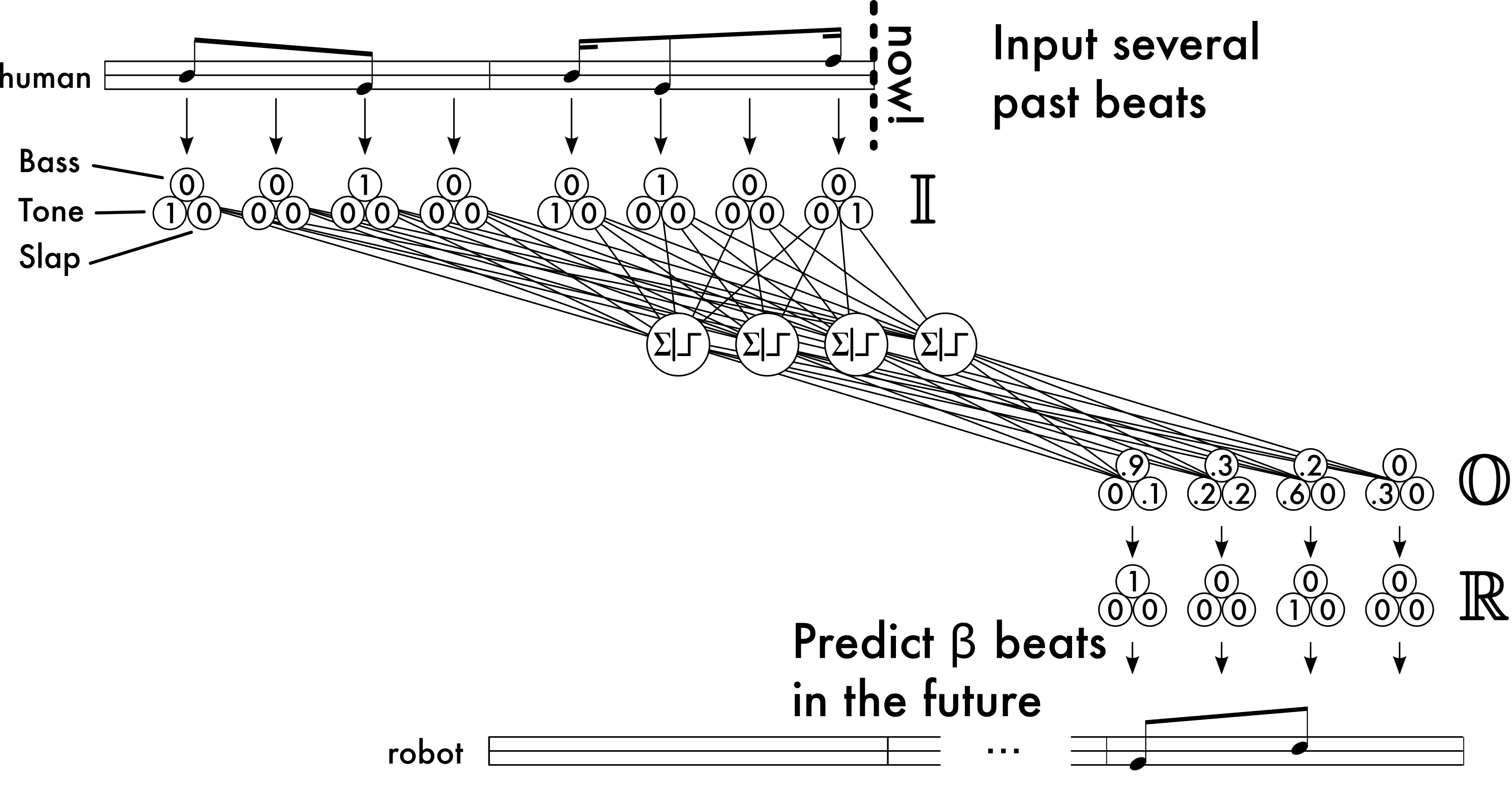
A rhythm, as executed on a given percussion instrument, is rarely understood to be simply a sequence of onsets distributed in time. At the very least, a rhythm is additionally understood to be a sequence of timbral categories. In the most general case rests may also be thought of as a possessing distinct timbre, although they shall not be modeled in the present study. For a hand drum, timbral categories are associated with particular methods of striking the drum, whereas for compound percussion instruments, such as drum kit, the timbre categories are additionally associated with particular drums. Previous work has shown that it is possible to classify these timbral categories in real time, as they are played by a human percussionist [64][71][67][70][72][68]. Consequently, timbre may be included in the model of the human's playing (i.e. the network inputs). Similarly, if the robot is capable of producing different timbres, then they may be modeled as well at the network output. This is accomplished by replacing each input and output neuron in the simple model with a cluster of neurons, each member of the cluster representing a discrete timbre. This arrangement is depicted in Figure 26.
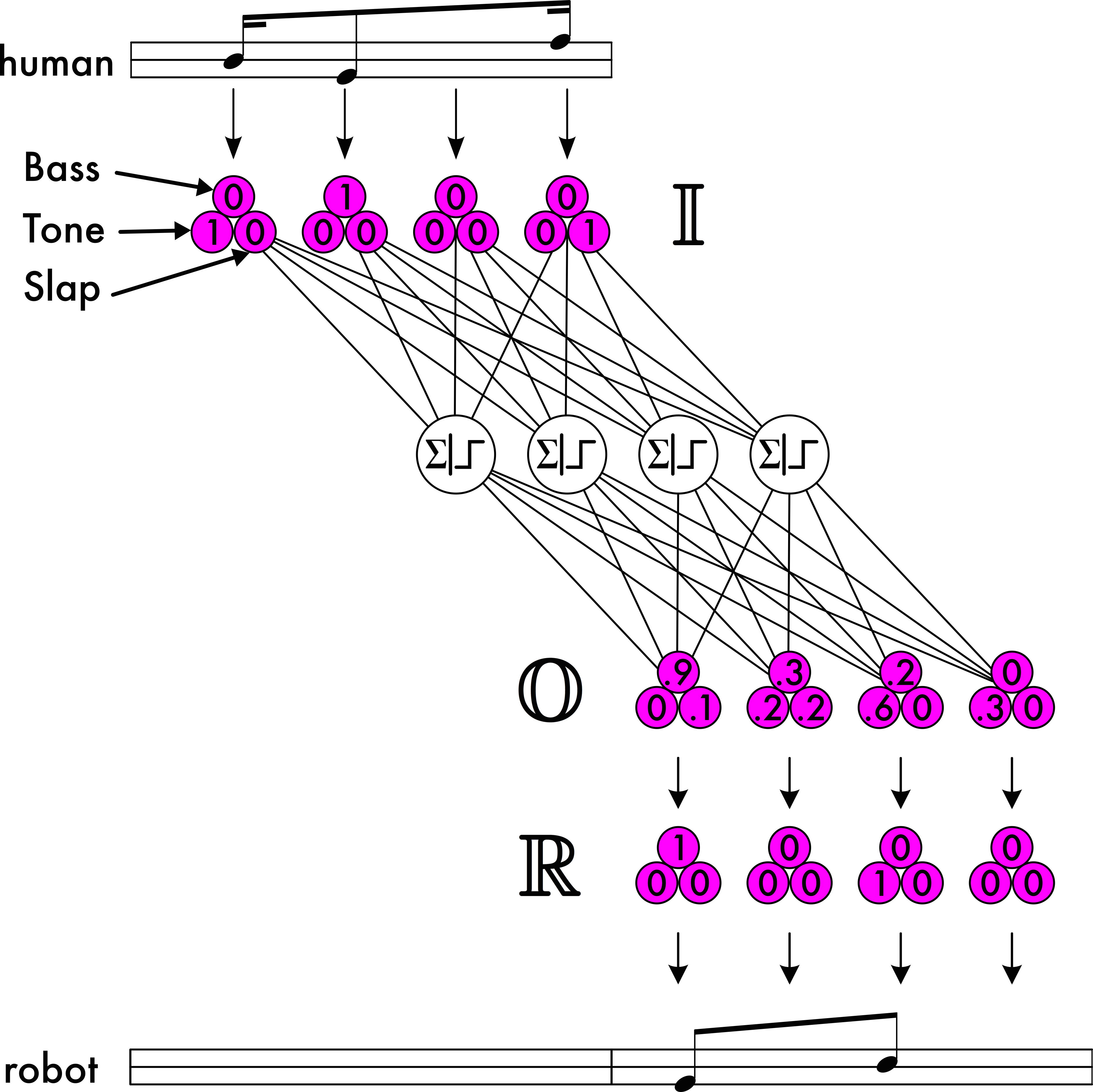
For the inputs, only those neurons that represent the timbre that the human played at the given timepoint are set to 1. During training the input clusters are mapped to the output clusters in such a way that at most one neuron in each output cluster is set to 1. If the number of input neurons per cluster is equal to the number of output neurons per cluster, i.e. if the human and robot are playing instruments with the same number of striking techniques, a one to one mapping bay be used. If not, other mappings may certainly be defined.
To interpret the network's outputs, a slightly more sophisticated statistical method must be adopted to determine what the robot should play. Suppose that the network output 𝕆 contains C clusters of neurons (one per timepoint), 𝕆 = {𝕆1, 𝕆2 …𝕆C}. Each cluster 𝕆c ∈ 𝕆 contains N neurons (each representing a timbral category), with activation levels of 𝕆c = {𝕆c1, 𝕆c2 …𝕆cN}. Let ℝ, also containing N neurons in each of C clusters, be the rhythm to be actually played by the robot, i.e. each ℝc contains 1 as a member at most once, and all other members are 0. Each activation level 𝕆cn is interpreted as the probability that the corresponding timbral category should be included in ℝ, referred to henceforth as P[𝕆cn] for simplicity, i.e.
| (1) |
| (2) |
| (3) |
6.3.2.2 Activation Function
Since valid values for output neurons lie between 0 and 1, it has thusfar been assumed, according to standard practice, that a logistic sigmoid function would be used for the output-layer activation. Notice, however, that this makes it impossible for the network to indicate that with 100% likelihood the robot should play nothing on a given timepoint. This is exacerbated by the presence of multiple neurons per cluster, because the neuron activations are summed, thereby increasing the probability of a spurious onset. Worse, if there are many timepoints per beat, this situation will occur frequently; even if the summed probability is small for a given timepoint, spurious onsets will be likely over time. So an activation function should be chosen which can explicitly represent 0. One option is a `truncated sigmoid', which is [1/(1+e−x)] when x is greater than some threshold, and 0 otherwise. This was found to significantly outperform the logistic sigmoid on all experiments presented in Section 6.4 below.
6.3.2.3 Timing
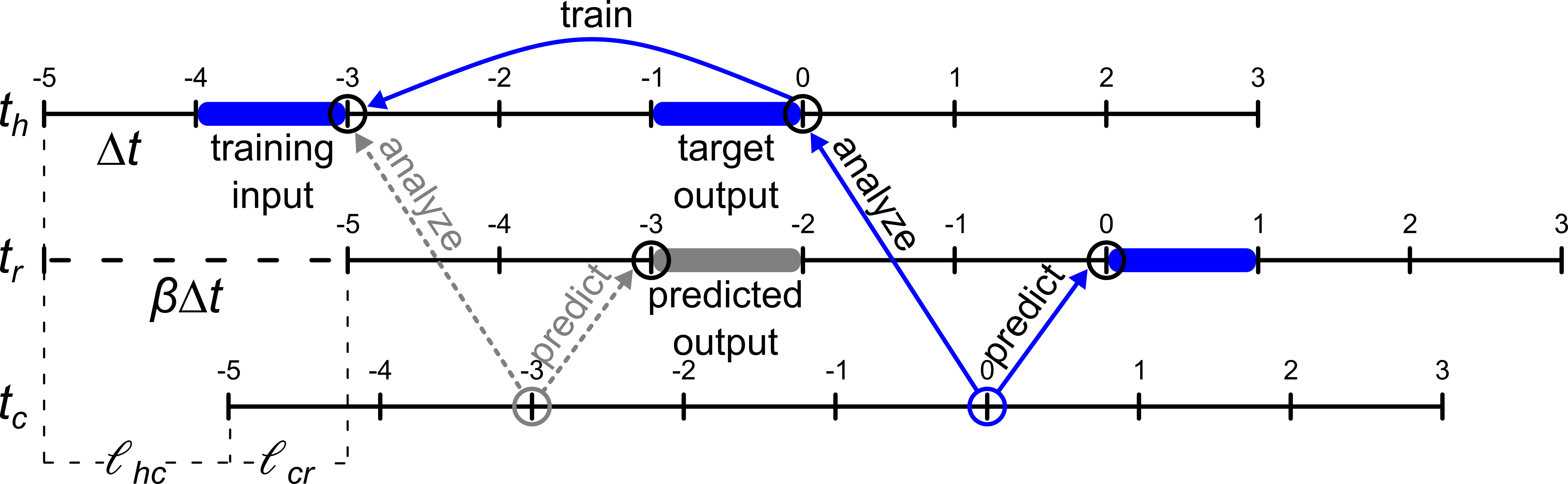
Predicting each beat at the very beginning of that beat assumes that the robot can strike the drum instantaneously if an onset is generated in the first timepoint of the predicted beat. A human cannot strike a drum at the precise moment they decide to do so, and it might not be realistic to impose that constraint on a robot. In other words, the robot has latency, which must be dealt with. More generally, all interactive systems contain multiple concurrent representations of the present, and latency is one manifestation of this phenomenon; from the user's perspective, the system's representation of the present lags their own. According to Einstein's theory of special relativity, it is in fact a basic property of nature that simultaneity is subjective and depends on the reference-frame of the observer. In systems where simultaneity from the perspective of the user is important, the typical approach is to reduce latency until it is nominally negligible. In the case of percussive robots, this approach is often not precise enough. Even very fast, fixed-position actuators have a latency ranging from about 10 to 70 milliseconds [17], and more dynamic mechanisms capable of moving about the drum and producing timbral nuances may have hundreds of milliseconds of latency (300 for Haile[15] and 600 for Kiki). By comparison, humans are relatively sensitive to small latencies - the temporal threshold between perceived simultaneity and perceived succession for two identical acoustic stimuli is about 32 - 60 milliseconds, depending on the individual and the experimental conditions [135]. Consequently, given almost any striking mechanism, it is not safe for designers of robotic percussion to assume that the robot can achieve perceptual simultaneity with the user by claiming that this latency is negligible. As a brief counterargument, it is worth mentioning that tactile stimuli on a human hand is perceived with about 30 ms more latency than auditory stimuli [135], so if humans base the timing of their own playing on haptic rather than auditory feedback, the robot could lag by an extra 30 ms before being perceptually late. It is reasonable to speculate, however, that percussionists base their timing primarily on sound rather than haptics (Evelyn Glennie may be a special case). In any event, in order to offset latency, percussive robots should decide what they are going to play some time in advance of actually playing it, lest they constantly lag. Given that the learning method presented here is inherently predictive, it can easily be modified to account for system latency.
Let the assumption be upheld that the music has a regular beat and the phase and tempo are known. In theory these constraints may be relaxed later by making the grid-spacing ∆τ very small; in principle the network should be capable of learning rotations of the rhythm relative to the training cycle and distributions of the strokes about the intended subdivision, although in practice such a network will require many more neurons and might take an impractically long time to converge. For a system with a single human and robotic drummer, let there be defined three representations of the present - th, tr, and tc. These are, respectively, the present as defined by the human, the robot's striking mechanism, and a computer which is receiving the human's input and sending commands to the robot's striker. From the human's perspective, these are all translated with respect to one-another. tr lags tc by some amount lcr which represents the entire latency between the computer sending a command and the sound of robot striking the drum reaching the human. The robot should typically be designed in such a way that lcr is constant. Furthermore, because a computer cannot act upon information until it has received and processed it, tc lags th by at least lhc_min. For the case at hand, in which the computer is receiving rhythms via a microphone, lhc_min must be a worst-case scenario estimate that includes maximum buffering uncertainty (refer to Appendix for a more detailed analysis of this), analysis latency (including the duration of audio required to perform stroke-classification) and, if rhythmic quantization is performed, the maximum unit of time by which a note could be quantized backwards to end up on the first timepoint of the beat (i.e. half of the grid spacing for grid-based quantizers). Additionally, the computer may deliberately introduce some arbitrary padding latency, so that ultimately tc lags th by a total amount lhc. If th must be in phase with tr (i.e. translated by an integer number of beats), padding must be introduced such that lhc is the total amount of time needed between the human striking the drum and the computer sending a command to the robot, such that the robot's stroke falls on the desired timepoint of a future beat, as heard by the human. It would be given by
| (4) |
In principle, the shorter lhc the better, because minimizing the temporal distance between the human and computer maximizes the amount of information that is available to the computer when it decides what the robot should play next. However, given a particular network topology and training strategy, the total number of beats separating the human from the robot β = [(lhc + lcr)/(∆t)] should not spontaneously change values according to the beat duration ∆t, but must be constant for the life of the network. This can be accomplished by choosing a desired β > = ceil([(lcr+ lhc_min)/(∆t)]), and defining a minimum allowable beat duration, ∆tmin, such that β∆tmin > = lcr Then, the appropriate lag is simply
| (5) |
Suppose the computer maintains musical time on a dedicated thread. Upon receiving the first downbeat from the human (after having obtained the beat-period and phase), it may introduce lhc − lhc_min seconds delay before starting the thread. It may then update the network every ∆t seconds and send commands to the robot every ∆τ seconds from thread start. Notice then that if the human's onsets are recorded in the human's timebase, they will need to be converted to the computer's timebase, by adding lhc, prior to use. The robot will convert to its own timebase naturally by introducing latency. This guarantees that if the human plays a stoke and the computer delays it for lhc seconds before repeating it to the robot, the robot will play a stroke β beats after the human's stroke.
A training scheme that accounts for these multiple representations of the present is depicted in Figure 27 and Figure 28. From the computer's perspective, the network still predicts what the robot should play in the immediate future, and learns from the immediate past. However, from the human's perspective, rather than predicting the robot's rhythm in the very next beat, the network predicts the rhythm β beats in the future. Then, β+ 1 beats later, the network is updated with what the human actually played in that beat. This necessitates three distinct steps at each training cycle. One forward pass through the network is made to predict the robot's output. Then, in order to put the network in the correct state for training, another forward pass is made using the beat that ended β beats previously as input. Subsequently, a training pass is made over the network, using the beat that just ended as the target output.
6.3.2.4 Long-term Dependencies
One very obvious and grave problem with the model presented thus far is that it only models temporal dependencies one beat in duration. In other words, it can only learn longer rhythms where each beat in the rhythm is unique. Formally, the problem is that feed-forward networks model functions, which map input to output, whereas rhythms might more properly be discrete dynamical systems, in which the current state (i.e. beat), and consequently the subsequent state, is determined by all past states. As stated in Section 6.1.4, RNNs are a family of very deep network topologies that model discrete dynamical systems with long-term temporal dependencies, which have been used to generate music offline and non-interactively. Recent optimization techniques have made them very powerful. Unfortunately, RNNs are not well suited to the task at hand. One problem is that they are very expensive to train online. The most common algorithm for training RNNs is Back-Propagation Through Time (BPPT), which assumes that the entire training sequence is known in advance, which will not be the case for online learning. The standard algorithm for training an RNN online is called, incongruously, realtime recurrent learning (RTRL). Incongruous because it has a time complexity of approximately O(N4) where N is the number of neurons, which makes it very impractical for realtime computation. Hessian-Free (HF) optimization speeds up training by reducing the number of epochs required. However, it does not help here, as HF is an efficient method of calculating how far down the error-gradient to step during each training cycle (i.e. replacing a constant learning rate), but the gradient would still need to be calculated at each time step, e.g. by using RTRL. Notice that the character-level language model discussed in the introduction, which uses a special RNN with gated neurons, and is trained with BPPT optimized with HF, still trained for five days on 8 high-end GPUs [104].
Another problem with RNNs for the current application is that the timing solution present in Section 6.3.2.3 above means that rhythm generation in this context is not causal. In other words, it is not possible, at each step, to train the current state before putting the network into the next state. Instead, because of the time-delay, training always occurs on a network state that is a few cycles in the past; this is essentially because a few cycles have elapsed while the robot was waiting to play. Of course it is in principle possible to save and subsequently restore past states for training, but by that time predictions have already been made based on future states, so reality effectively bifurcates at each training cycle, and it is not clear which branch to follow. It may or may not be possible to design a non-causal dynamical neural network, but further investigation shall be left for future work.
So in order to expand the temporal range of the network, the feedforward model is upheld, but more input neurons are included to encompass several past beats. At each training cycle (the beginning of each beat), the input vector is shifted one beat to the left, and the rightmost input neurons are populated with the most recently concluded beat. This entire vector is propagated through the network to produce the next beat of output. This is shewn in Figure 28. Training occurs as before.
6.4 Evaluation
A set of experiments was performed to assess the network's ability to learn both specific rhythms and the musical character of improvisation. These experiments were carried out using two types of methodology. One type consists of strictly numerical analysis, whereby encoded rhythms were fed into the network offline, and its outputs were analyzed statistically. The other type involves the realtime input and output of sound. In this latter type, contact-mic recordings were made of the core djembe strokes, and audio-editing software was used to arrange these into audio files containing metronomically precise rhythms. These recordings were played into the realtime onset-detector and stroke-classifier described in [64], which was trained to classify these particular strokes with 100% accuracy. Onset times were ascertained by examining the audio-buffer timestamps and counting samples into the buffer to where the onset occurred. The first two strokes in the constructed file were used to define the tempo, and subsequent strokes were quantized using a simple grid-based quantizer. The quantized strokes were then fed into the network in real-time, one beat at at time. The network outputs were either sent to the robot to be played in realtime, one timepoint at at time, or to a software simulation of the robot which delays incoming messages by 600 ms before playing a recording of the stroke. These two types of methodology are functionally identical and were used interchangeably during software development. This software can receive live input from a human just as easily as a constructed audio file. However, in the absence of robust tempo-following and quantization, the software is rather inaccurate at transcribing human performance, which makes it difficult to isolate the network's behaviour. Because accurate transcription was not a goal of this study, assessment with live human input was not performed.
6.4.1 Network Topology
In all of the following studies, the network had three stroke categories in both the input and output rhythms (understood to be bass, tone, and slap), twelve timepoints per beat, 6 input beats (i.e. 216 individual input neurons), 1 output beat (72 neurons), and a single hidden layer with 9 individual neurons. The output layer used a truncated sigmoid activation function as described in Section 6.3.2.2 with threshold −4, and the hidden layer used softplus (ln(1+ex)). Output is predicted two beats in advance, i.e. β = 2. In each experiment, the only model parameter, the learning-rate l, was chosen by trial and error to be approximately optimal for the given task.
The network shall be said to have `learned' a rhythm when the robot is 95% likely to play that rhythm in response to a particular input. This is defined as follows. Let 𝕆cn be the activation level of the nth neuron in the cth cluster in the output rhythm, let ℝcn be a binary value representing whether the robot actually plays the nth timbre at timepoint c, and 𝕋cn is the same in the target rhythm. The probability P(ℝ = 𝕋 | 𝕆) that the robot will actually play the target rhythm is defined to be
| (6) |
6.4.2 Learning Specific Rhythms
The first set of tasks involves learning specific rhythms that are played repetitively by the human. The goal of this is to ascertain the degree to which the network can learn when it is very precisely appropriate to play specific timbres. The dataset used in these tasks comprised all of the repeated djembe rhythms in [136] (i.e. the parts labelled `djembe 1', `djembe 2', etc..., but not `signal' or `introduction' or parts for other instruments). At times, the djembe serves an accompaniment role, so certain common accompaniment patterns appear in several pieces; such rhythms were only included once. This resulted in 66 unique rhythms ranging in length from 1 to 16 beats (mean 3.79), and containing a mixture of simple and compound meter (as written). Beat groupings were used as given by the beaming in the text, although it is worth noting that the Western conception of `beat' is not entirely applicable to West African music, and this represents only one of several possible encodings of the rhythms; another encoding might involve keeping the duration eighth-notes (quavers), instead of the beat, constant across rhythms. Some rhythms were written with superfluous repetitions, e.g. a 2-beat rhythm written twice to fill four beats; the superfluous beats were discarded. The few instances of unusual strokes in the data were replaced with one of the core three. The network was tested with this dataset on three tasks, to be presently discussed; results are summarized in Table 8.
| Experiment | Unit of Result | Result |
| Individual Rhythms | Number of repetitions required to learn a rhythm | 14.32 |
| Corpus of Rhythms | Number of repetitions required to learn and retain 65 rhythms | 106.5 |
| Signal Rhythm | Probability of playing correct rhythm following a signal | 96% |
6.4.2.1 Individual Rhythms
In the author's experience playing in community drumming ensembles in the United States, a common musical piece consists of most members playing a single accompaniment rhythm in unison, repeated ad infinitum, while a select few members play counter-rhythms or improvised solos. Several such pieces may be played during a single rehearsal or performance. Can the robot learn to play the accompaniment rhythms in this scenario? Can it do so in a reasonable length of time? Assessment of this task was performed by initializing the network weights, and repeatedly feeding a rhythm from the dataset into the network one beat at a time. Here, the rhythms are taken out of context and assumed to have been repeated infinitely, so even during the first training cycle, inputs representing past beats were populated with previous repetitions of the rhythm - i.e. each rhythm was rotated through the network. Then, learning duration was measured by counting the number of times the rhythm was rotated through the network in its entirety before it had been learned. This entire process, starting with initializing the network, was repeated for every rhythm in the dataset (N=66) and the results were averaged across rhythms. That entire process was repeated 10 times and the averages were averaged. With l = 0.65, the mean learning duration was 14.32 repetitions of the rhythm (N=10, σ = 1.52). In the cited scenario, the network weights would have to be manually initialized between pieces to achieve these results. If the weights are not initialized in between pieces, it takes a little longer to learn each rhythm. In a test that initialized the network before the first rhythm, but not subsequently between rhythms, using l = 0.5, the average duration was measured to be 21.42 repetitions of the rhythm (N=10, σ = 2.760955). On the one hand, this is very feasible, as it takes only 42 seconds to repeat a 4-beat rhythm 21 times at 120 beats per minute. On the other hand it may be tedious to repeat a rhythm 21 times to a robot. Note however that the definition of `having learned' a rhythm is relatively stringent; the network is capable of representing 7.9×1028 unique 4-beat rhythms, and it is thus extremely unlikely that the network will output the correct rhythm by chance alone, yet the given definition specifies that such will happen 19 times out of 20. A more relaxed definition would be that the network has `learned' a rhythm after each neuron is 95% likely to output its target value. Repeating the last experiment with this relaxed definition and l = 0.3 yields a mean of 9.87 repetitions of the rhythm (N=10, σ = 0.68). With such a definition, it is not likely that the network will output the correct rhythm precisely, but it is significantly more likely than random to get each timepoint correct, which should produce something that resembles the rhythm. In other words, after hearing a new rhythm only a few times, the network should sound like it is starting to get the gist.
6.4.2.2 Corpus of Rhythms
This shows that a previously-untrained network can learn individual rhythms, but can it also retain rhythms it has learned? In a more standard machine-learning scenario the network would be pre-trained with a corpus of rhythms prior to human interaction, either by offline training or by previous online interaction with humans. Can the network learn a corpus of rhythms? The same 66 rhythms as above were used to test this. Here, after initializing the network and training it to output zeros, each rhythm was rotated through the network in its entirety once, one after the next, round robin, until all rhythms had been learned. Indeed, on average, the network learned all of the rhythms after hearing each rhythm 305.50 times (l = 0.15, N=10, σ = 158.55). Longer rhythms take longer to learn, according to Equation 6.6; in the current dataset one outlier rhythm was twice as long as any other, and this one always took much longer to learn than the others. Excluding it from the dataset resulted in a mean of 106.50 repetitions of each rhythm (N=10, σ = 11.38). The convergence rate, in general, could probably be improved using standard techniques (annealing, scrambling the order on each cycle, Newton's method, batch learning, etc...), although here the goal was to demonstrate that the network is capable of learning when to produce certain timbres across a large variety of contexts - offline batch learning with maximum efficiency was not the primary goal.
If the only goal were to learn specific rhythms, it would of course be faster and more precise to simply transcribe what the human plays, hash it, and store it in a database. Some advantages of the method presented here are as follows: this method is agnostic to the length of rhythmic patterns so it is not necessary to explicitly segment the pattern boundaries; neural networks tend to be impervious to small variations in input, as may arise as the result of transcription error or creative variation; fuzziness at the output may be desirable to alleviate monotony - because a trained network contains a statistical model of the human's playing, this fuzziness may be accepted as musically interesting variation.
6.4.2.3 Signal Rhythms
Another task not suitable for database lookup is predicting changes in the music according to context. Often in the rhythmic music of Africa and Latin America, special rhythms are used to signal musical changes. A good example comes from a pair of rhythms in the dataset, called Yankadi and Makru, which are used in a courtship dance. The basic Yankadi rhythm is repeated many times while men and women dance facing each other in rows. After an arbitrary number of repetitions, the drum leader plays a signal rhythm (either on a whistle or a drum) which signals the switch to Makru. At this time, the dancers begin dancing in pairs, while the drummers repeat the Makru rhythm many times. Eventually, the leader plays the signal again, which prompts the transition back to Yankadi, and so the piece continues, alternating Yankadi and Makru for the duration of the evening. These rhythms are depicted in Figure 29. So, the signal rhythm could be followed by either Yankadi or Makru, depending on the context (i.e. what rhythm was previously playing).
Can the network learn and retain the ability to predict what the human will play following the signal? This was tested as follows. A numerical sequence was constructed comprising 3 repetitions of Yankadi, followed by the signal, followed by 3 repetitions of Makru, followed by the signal again. Three repetitions are the minimum such that the network cannot learn this sequence as a single rhythm, i.e. every six beat window is not unique; in other words, the network can not know in advance whether the human plans on playing the signal or another repetition of the current rhythm. This rhythm was used to train the network with l = 0.1 until the least accurate output neuron over the whole sequence was at least 40% accurate (roughly meaning that it was about 40% accurate in guessing whether the human would branch to the signal or continue repeating the rhythm). Then, an audio recording was constructed which contained an arbitrary number of repetitions of each rhythm (always 8), each followed by the signal. This audio file was fed into the network and conceptually paused after the signal, at which time the network had already predicted the next two beats. The probability that the predicted two beats would belong to the correct rhythm was calculated again according to Equation 6.6. This process was repeated 20 times (10 transitions to each of Yankadi and Makru). On average, the probability that the network would output the first two beats of the correct rhythm was 0.96 (N=20, σ = 0.029). During this test, the network continued to learn online from the input sequence with a rate of 0.1. As learning goes hand-in-hand with forgetting previous information, one might predict that the extra repetitions of Yankadi and Makru in the test sequence would have caused the network to forget the meaning of the signal in the meanwhile. On the contrary, no significant change in accuracy was observed over time (it actually increased marginally), even though this task updated the network weights 720 times during testing (there were that many beats in the input sequence). In many musical situations, it may be appropriate for the robot not to play the same rhythm as the human, but to always accompany rhythm a with rhythm b. In principal, two human percussionists could train the robot to exhibit this behaviour, if one human's rhythm was used as the network input and the other human's as the target output.
6.4.3 Learning Improvisation
The preceding section treats the network's ability to learn specific, repeated rhythms. In a different scenario, a human may improvise rhythms with no explicit structural repetition. In that case, the robot would not be expected to play in unison with the human, but should instead either match or deliberately oppose salient characteristics of the human's music. Three tasks were used to assess the network's ability to do this, as will be presently discussed, and the results are summarized in Table 9.
| Experiment | Unit of Result | Result |
| Note Density | Correlation and slope of regression line for input vs. output note density | r=0.977; m=1.0 |
| Meter | Probability of playing on an incorrect timepoint | 0.0039 |
| Syncopicity | Correlation and slope of regression line of input vs. output syncopicity | r=0.96; m=0.80 |
6.4.3.1 Note Density
One such character is the note density, d, of the music, which may be defined here as the number of onsets divided by the number of timepoints in a given span of music, or, if rhythms are statistical, d = ∑c=1CP[𝕆c] / C. Very sparse rhythms may have a different aesthetic character than very dense rhythms, and in many cases it would be appropriate for the robot to match the human's d. Consider a scenario wherein the human improvises a rhythm with a particular character and corresponding d for a while, and after some time begins improvising with a new character and corresponding d. Can the robot adapt to this change? This was tested as follows. First, a very long rhythmic training sequence was constructed comprising 6000 beats. For each 120-beat segment (representing one minute of playing at 120 BPM), a random d was chosen, and a random rhythm was generated in that segment by, with a probability of d, populating each timepoint with an onset in a random timbral category. The resulting sequence then contained 50 such concatenated segments. To train the network, the entire sequence was shifted through the network, to simulate previous interaction with a human. Then a new 6000-beat validation sequence was constructed by the same means, and shifted through the network. At each beat of the validation sequence, the observed rhythmic density of the network input (previous 6 beats) and predicted output (one beat) were recorded and subsequently correlated. The input density and output density were found to be linearly correlated with r = 0.977, and the regression line had a slope of 1, meaning that the network is very good at matching the note density of improvised rhythms. In certain scenarios, it might be desirable for a robot to oppose the human's d rather than mimic it, such as when a foreground musical role in one part should be paired with a background role in the other part; the described method does not present an obvious way of achieving this.
6.4.3.2 Meter
Another salient characteristic of rhythm is its meter. In particular, in most cases, the human's decision to play in either simple or compound meter should be matched by the robot. Simple meter is characterized by a binary or quaternary subdivision of the beat with onsets on the 1st, 4th, 7th, 10th timepoints (i.e. 16th notes or semiquavers) of any beat, whereas compound meter uses a tripartite subdivision with onsets occurring on the 1st, 5th, and 9th timepoints (triplets). These shall be referred to as the `valid' timepoints for the corresponding meters. The network's ability to match the input meter was tested as follows. A training set of 1000 6-beat rhythms was constructed for each meter, by randomly populating the respective valid onsets with an average note density of 1 onset per beat. Each rhythm was rotated through the network once, alternating meters. Then a validation set of 100 6-beat rhythms in each category was similarly constructed and rotated through the network. Because meter is defined by those timepoints where onsets should not occur, the probability of playing on at least one invalid timepoint was measured for each beat of output, and averaged across all beats. On average, the network produced output on an invalid timepoint with a probability of 0.0039 (N = 1200, σ = 0.029). Although this is reasonably low, notice that it took a very large number of training cycles to achieve. With much less training, the network will begin producing invalid onsets with a probability of exactly 0 on the majority of beats, but will spuriously produce a relatively high probability, distributed in small quantities across all invalid neurons, on a handful of beats. More training reduces the frequency and value of these spuriously high probabilities, but does not seem to eliminate them. So although the network can match meter given enough training, it does have trouble producing output of exactly 0 on specific timepoints.
6.4.3.3 Syncopicity
Yet another salient characteristic of rhythm is syncopicity, s, which is a measure of how syncopated a rhythm is. This experiment considers only the 1st, 4th, 7th, 10th timepoints of any beat, referred to collectively as the `valid' timepoints, whereas the 4th and 10th specifically are considered the syncopated timepoints. Here s shall refer to the rhythmic density defined over the syncopated timepoints divided by the rhythmic density defined over the valid timepoints for a given span of rhythm. Random sequences with given s were constructed by, with probability s, populating syncopated timepoints with an onset in a random category, and doing so with a probability of 1−s in other valid timepoints, resulting in an overall note-density of 0.5. The network's ability to match syncopicity was tested as for note density, i.e. a 6000-beat training sequence followed by a 6000-beat validation example, with 120-beat segments with random r. Output syncopicity was 96% linearly correlated with input syncopicity. The slope of the regression line was 0.80 indicating that although the network was very good at matching s, it has some trouble producing extreme values of s. This is consistent with the results of the meter test above, which suggests the network has some trouble outputting exactly 0 on specific timepoints.
6.5 Conclusion and Future Work
The algorithm's ability to quickly learn a statistical model of repeated rhythms demonstrates that it learns the contextual use of timbral categories as used by a human. That it can learn other features in improvised contexts demonstrates that the resulting music will in some sense be stylistically appropriate.
In the future, the work presented in this paper should be tested with human interactors. How does this method compare to playing with another human, or alone, or to a robot that generates random rhythms, non-interactively? Does this method feel responsive? If users had a percussion robot employing this algorithm at home, would it encourage them to play longer or more frequently than they would otherwise? Will fuzziness at the robot's output be interpreted as creativity or mistake?
