TIMBRE PRODUCTION
Attempts to automate percussion playing date back at least to the Islamic Golden Age [25][26][27]. In these automata, a striking mechanism is driven into a drum via a complex system of levers, water-wheels, and gravity. However, due to limitations in the mechanics, the striker always falls upon the drum in the same way, producing the same timbre. By contrast, the dynamic manipulation of timbre is central to how humans play drums; for example, the famous djembefola Famoudou Konaté reports being able to produce approximately twenty-five distinct timbres [45]. In fact, the word `timbre' comes from the Greek word for `drum', and for many drums, especially hand drums, timbre is the primary parameter that the player manipulates while playing (as opposed to pitch for the majority of orchestral instruments). In recent decades, many more percussion robots and automata have been built [5][8][46][47][48][49][50][51][52][53][7][54]. Although levers, cables, and gravity have been replaced by solenoids, servos, and electricity, the majority of these still drive fixed-position drumsticks or mallets into a drum with little or no control over timbre. One notable exception is Haile [47], one of whose strikers can move along the drum's radial axis, striking it in different locations. Prior to the addition of this capability, the authors reported that "the main mechanical caveats mentioned were Haile's limited timbre and volume control" [15]. Another notable exception is MIT's Cog, which, when outfitted with special arms with compliant actuators [50], was able to exploit the arms' natural dynamics in striking a snare drum, perhaps modeling more closely the way humans strike snare. However, the timbre of sound produced by this method was not within the purview of the study and was not assessed. To the best of the author's knowledge, no percussion robot has been designed specifically with the aim of dynamically producing a variety of timbres that are similar to those produced by human players. Therefore, the author has built a djembe-playing robot named Kiki (shown in Figure 1), specifically with this goal in mind. Here, the thought-process behind Kiki's design is presented as a case-study in how timbre might be approached more generally in musical robots. The first half of this paper will focus on the material properties of the striking mechanism which influence timbre, including the solution eventually used in Kiki. The second half shall focus on actuating the striking mechanism, given the particular challenges associated with dynamic timbre production.
Insofar as the goal is to produce human-like timbres, it is fruitful to take a biomimetic approach, and examine how humans achieve different timbres. As previously mentioned, a skilled djembe soloist may produce a wide variety of distinct timbres; certainly this repertoire could be expanded even further if the possibility of striking the drum with arbitrary objects were included. However, djembe accompaniment technique comprises three core strokes with aurally distinct timbres: bass, tone, and slap. Players typically evaluate the sound of a djembe by evaluating these three strokes [55]. It is therefore justifiable to focus on building a machine that can reproduce the timbre of these strokes, although the goal is to do so dynamically (i.e. rather than using three fixed beaters) so that the machine will be capable of playing other intermediate timbres and searching its timbre space for particular sounds. Below are descriptions of the striking technique for each stroke, which are informed by the descriptions given in [45], an analysis of a video of the djembefola Mamady Keita demonstrating the strokes [56], and the author's own experience playing the instrument.
The center of the drum is struck with an open hand, as is illustrated in Figure 8(a). The fingers are slightly hyperextended so that the pressure is concentrated on the palm. The precise location of impact depends on the precise shape of the drum, the speed of the passage being played, and the player's preference, but the overall goal appears to be to excite the head in its first radial normal mode. The result is a deep, resonant, sustained bass sound with few audible higher partials.
Many verbal descriptions of djembe technique often indicate that tone is played by striking the drum such that palmar-digital crease falls upon the rim of the drum. In the video used for this analysis, however, the player's entire hand is shifted more towards the center of the drum, such that the medial extremity of his proximal palmar crease is clearly seen in contact with the rim. This is shown in Figure 8 (b). The four fingers are held straight and somewhat rigidly. In the video, the palmar crease is seen contacting the rim slightly before the fingers contact the head. The four fingers are parallel to the head at the moment of impact and strike it with uniform pressure across their length.
The hand strikes the drum at a slight angle, with the fingers held loosely in a slightly curved position. In slow motion, the stroke has two discrete components, illustrated in Figure 9. First, the distal palmar crease and the medial extremity of the proximal palmar crease come into contact with the rim. Second, inertia causes the fingers to bend about the metacarpophalangeal joint so that, a very short time later, the fingertips and only the fingertips contact the drum head. Video analysis reveals the palm touching the rim in one frame, and the fingertips have just rebounded by the next frame, so the interval is on the order of about 40 milliseconds.
Percussion robots are often built to be capable of striking the drum at several radial distances from the center of the head [46][14][15]. However, the foregoing analysis makes it clear that the strokes in question differ by more than just the impact location. Below is a discussion of some other factors that may contribute to the distinct timbre of each stroke.
The hyperextension of the fingers during bass indicates that the fingers are rigid, while during slap the fingers must be loose so that they may be under the control of inertia just before and after impact. During tone, the fingers appear to have an intermediate rigidity. This suggests that the a robotic beater could benefit from variable rigidity.
Fourier analysis of the time evolution of vibrating bodies in general makes it clear that the shape of the perturbation that set the body in motion plays a large role in the frequency content of the resulting sound. The same principals hold for vibrating membranes as for strings. A circular membrane with a zero-displacement boundary condition about its circumference has two types of nodal lines, which define the normal modes [57]. The first type forms concentric circles about the center of the drum, and the height of any concentric circle varies sinusoidally. The other type of nodal line runs radially outwards from the center of the head. The height of any other radial line forms a Bessel function of the first kind with a zero-crossing falling on the drum's boundary. This is illustrated in Figure 10.
The part of the human hand used in the tone stroke is roughly wedge shaped, and roughly four inches in breadth at its base. A typical djembe (including the one used in this study) has a circumference of about forty inches. The hand therefore fits comfortably into a radial sector of the head that is about a sixth of its total surface area. One may therefore hypothesize that the sixth radial normal mode plays a prominent role in the sound of the tone. If the hand were rectangular, so that the index, ring and pinkie finger were equal in length to the middle finger, and the fingers were not tapered, and so forth, then the extreme end of the hand would cross the nodal lines of the sixth normal mode, thereby suppressing it. The hand, in turn must suppress even higher radial normal modes, which an overall narrower object would not. Likewise, the palm of the hand is roughly round, and roughly a quarter of the diameter of the head. During the bass stroke it tends to push the head downward roughly into the shape of a parabolic dish, exciting the first and possibly second concentric normal modes while suppressing the radial normal modes and higher order concentric modes. A much smaller circular object would allow higher concentric modes to sound. Any fat, rigid object with corners would exert more force at the corners than its center as the head deforms downward, which would tend to excite the radial normal modes. It thus follows that an object whose surface of contact is similar in shape to the hand will be better suited to recreating the timbre of the hand than an arbitrarily-shaped object. Note that the foregoing analysis focuses on the normal vibrational modes, which are steady-state solutions to the wave equation. However, because of the steep amplitude envelope of percussive sounds, which focuses much of the sound's power in the first few milliseconds of vibration, transient solutions to the wave equation may play a large role in the perceptual qualities of the stroke. Although the transient motion of a circular elastic plate with a zero-displacement boundary condition along its circumference in response to loading on a radial sector has been studied [58], it is not clear what frequency content emerges from this motion. However, the nature of the transient motion will still be determined by the shape of the initial perturbation, and consequently the shape of the hand is likely to be important in determining the resulting sound.
Slap is often considered the most difficult of the three strokes for a beginning human player to produce, and has proven difficult to mechanize. We thus present some additional information that may be useful in this regard.
Drum-to-hand size ratio is important for the production of slap. Sunkett makes the following observation.
This [slap] is not an easy sound to achieve on every drum, and the ability to do so is often related to the diameter of the drumhead and the size of the players's hands. If you have small hands, the drumhead diameter does not have to be very large to achieve the sound without too much effort. Larger hands requite larger head diameters... There are perceivable frequency differences in the resultant sounds. The highest overtones used to produce a dynamic slap are most easily activated near the edge of the drum [
55].
Presumably the drum-to-hand ratio must be large so that the hand can excite the higher radial normal modes while suppressing the lower ones, and the edge of the drum is used to excite the higher concentric normal modes.
Beginners are sometimes taught to play tone with the fingers together, and slap with the fingers apart. This artifice is perhaps designed to regulate the flexibility of the fingers, taken as a single unit. Keita reports that although he teaches the strokes this way, he plays both strokes with his fingers slightly apart [59].
In Sabar ensembles of Northern Senegal, a variety of open-bottom drums are played that are roughly similar, in limited respects, to djembe. A consideration of their technique lends insight into how the slap sound on a djembe may be mechanized. (The following discussion is the result of personal correspondence with the late Dr. Mark Sunkett). In contrast to the djembe, which is played with two bare hands, the drums of the Sabar ensemble are played with one bare hand (traditionally the left) and one stick, known in the Wolof language as `galan', held in the other (right) hand. The bare hand generally plays the three strokes associated with djembe, using similar technique, while the stick typically plays only one stroke. Anecdotally, native players report that the sound of the slap played by the bare hand should sound identical to the sound produced by the stick. The stick is made either of Tamarind, which is a hardwood of the Leguminosae family, or an indigenous wood, called `sump' in Wolof (Balanites aegyptiaca), which is somewhat softer and more flexible. The stick is typically about sixteen inches long and very roughly 3/8 inch in diameter, although the ideal diameter varies somewhat proportionally to the size of the drum being played. The stick is prepared for use by removing the bark and rounding the ends with a knife. Ideally, the stick is slightly bowed on one end and, while playing, the stick contacts the drum head along the convex edge of the bowed segment. The stick is held loosely in the hand, oriented perpendicular to the fingers. It is actuated by rotating the forearm about the roll axis, so that the stick moves similar to a windshield-wiper. This arrangement is certainly mechanizable, although subsequent analysis reveals that it may not be dynamic.
The goal of the foregoing discussion was to consider what factors might contribute to an object's timbre when used as a striking mechanism, and in particular, what objects might sound most like the hand or produce the greatest range of timbres when striking the drum. In order to provide greater insight into how these factors might influence the design of such a beater, timbral evaluation of several objects was carried out. The purpose of this study was exploratory, and no hypothesis is proposed.
In this study, various objects, including human hands, were used to strike the drum in various ways. The resultant sounds were recorded and compared against each other. This was carried out as follows: A particular object and method of striking the drum with it were casually identified as being worthy of analysis by the author on account of the foregoing discussion; Several recordings were made of the object striking the drum in a particular way; All recordings were made during the same recording session, with the same placement of microphones and drum, so as to control for the placement of microphone, and acoustics of the room; The recordings were edited such that the first sample in the file corresponds to the zero-crossing marking the onset of the sound; The recordings were then analyzed and compared.
A variety of objects of different materials were tested during this study. They included various drumsticks, mallets, pieces of foam, rubber, cork, and linoleum. They were at times used alone, and at times mounted to a flat or convex wood or rubber block. Only a subset of these objects are reported here. The materials reported are a hickory drumstick, a sheet of 1/4-inch black rubber cut roughly to the outline of a human hand, and a large piece of foam rubber in the shape of a fist. These objects are depicted in Figure 11. They were used to strike three locations on the drumhead, corresponding roughly the three strokes under consideration. The locations were the center of the drum, the `edge' of the drum (approximately three inches from the boundary of the drumhead) and the `rim' (approximately one inch from the boundary).
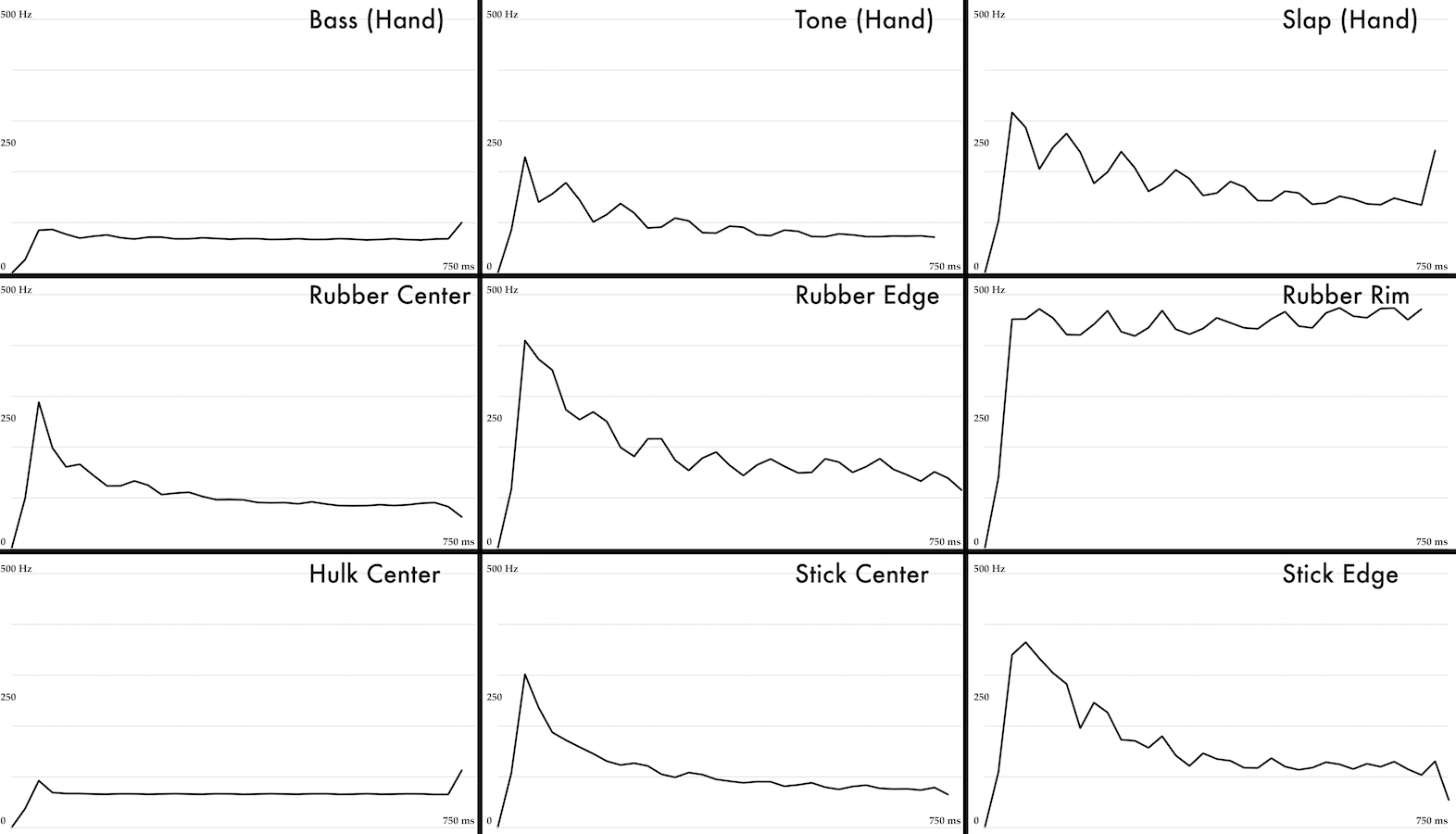
Machine representations of timbre that correspond to perception are an area of ongoing research. One seminal study [60] found that humans rate timbral similarity according to three dimensions, corresponding roughly to attack quality (explosiveness), the temporal evolution of spectral components, and brightness (strength of higher partials). A similar study, focusing specifically on on percussion found similar results [61]. Moreover, djembe players almost universally describe bass, tone, and slap as being low, mid, and high, respectively, suggesting a difference in perceptual brightness. Furthermore, a drumhead's normal modes are of course determined by its geometry; perturbing it in a particular way merely distributes the energy amongst those modes in a particular way. Spectral analysis, as can be seen in Figure 12, confirms this, indicating that for bass, relatively little of the energy is in the higher partials. Tone is intermediate, and slap has relatively little energy in the lower partials.
This suggests the use of spectral centroid (weighted average) [62] as a preliminary measure of timbral similarity, which has also been shown to correlate with perceptual brightness [63]. It is important to point out that this by itself would not be an appropriate way of comparing timbre across instruments because two sounds with dramatically different frequency distributions could produce the same centroid. Indeed, a more general approach involving higher-order spectral moments (describing the shape of the frequency distribution) shall be presented in Chapter 4 of this dissertation. In the case of the membranophones, however, it does not appear to be possible to control the frequency distribution independently of the centroid. Therefore centroid is used as follows.
Given a discrete signal x of a drum sound, x is separated into M windows W = {w1, …wM}, each containing N consecutive samples and each successively translated in x by a hop-size of h samples. First, the Fourier Transform X of each window is computed. Then, the spectral centroid C for a given window w ∈ W is the amplitude-weighted average of X across all frequencies ω.
|
X(w, ω) = |
N−1
∑
n=0
|
w[n]e−[(j ω2 πn)/N]; C(w) = |
|
; |
| (1) |
In particular this study uses a window size N=1024 and a hop-size of h = 512 samples. For each stroke, only the first 750 milliseconds of audio after the onset were used because, although the drum still audibly resounds for some time beyond that, the signal-to-noise ratio becomes too low and the variance in the centroid becomes high. The sound of a particular stroke may have a certain amount of variability, as it cannot be performed identically each time. In order to address this, for each object and strike location, C(w) is computed for three separate instances of the stroke and averaged point-wise over W. The results are plotted in
Figure 13.
Given two drum sounds each separated into their respective windows W1 and W2, the sounds are compared using the standard deviation σ of one with respect to the other over the windows w. Additionally, the base-2 logarithm and 12th power of the centroid, ℂ, are used so that the result is expressed in semitones.
|
σ = ± |
⎛
√
|
1
M
|
|
M
∑
i=1
|
(ℂ(wi ∈ W1) − ℂ(wi ∈ W2))2 |
|
|
| (2) |
Additionally, the positive or negative solution to the square root is chosen according to

This allows the metric to retain some information about which sound is perceptually higher. In this manner each sound is compared to each other sound. Comparing the average of three tone strokes to the average of three separate tone strokes yielded σ = 0.9. This was taken to be the resolution of measurement and all values were rounded to the nearest integer. The results are shown in Table 1.
Table 1: Timbral comparison of striking materials. To determine the signs, rows were used as W1 and columns as W2
| | Bass (Hand) | Tone (Hand) | Slap (Hand) | Rubber Center | Rubber Edge | Rubber Rim | Hulk Center | Stick Center | Stick Edge |
| Bass (Hand) | 0 | -8 | -17 | -9 | -18 | -32 | 2 | -10 | -16 |
| Tone (Hand) | 8 | 0 | -11 | -3 | -13 | -27 | 8 | -3 | -10 |
| Slap (Hand) | 17 | 11 | 0 | 9 | -3 | -16 | 17 | 10 | 4 |
| Rubber Center | 9 | 3 | -9 | 0 | -11 | -25 | 10 | -2 | -17 |
| Rubber Edge | 18 | 13 | 3 | 11 | 0 | -15 | 19 | 10 | 4 |
| Rubber Rim | 32 | 27 | 16 | 25 | 15 | 0 | 33 | 26 | 19 |
| Hulk Center | -2 | -8 | -17 | -10 | -19 | -33 | 0 | -10 | -16 |
| Stick Center | 10 | 3 | -10 | 2 | -10 | -26 | 10 | 0 | -8 |
| Stick Edge | 16 | 10 | -4 | 17 | -4 | -19 | 16 | +8 | 0 |
There were far too many confounding variables in this study to make predictions about what timbre will be produced by a given object. In addition to the considerations in Section 3.2.2, other properties such as mass, softness, coefficient of friction, impact velocity etc... appear to be important. Nonetheless, the aim of this study was only to provide the tools and a starting point for exploring those properties in greater detail. In any case, a few observations may be made regarding the above data. The stick is capable of producing sounds that are relatively similar to tone and slap. This is consistent with the discussion of sabar technique above. However, it cannot produce a variety of timbres. In this study, the hand had a range of about 17 semitones (bass compared to slap), whereas the stick's range was less than half or that (edge compared to center). In particular, the stick could create a sound with a low centroid similar to bass stroke, which is consistent with the observations about hand morphology. The rubber sheet could also produce sounds similar to tone and slap, and additionally had a range of 32 semitones (center to rim), which is nearly twice as large as the hand. However this range extended the range of the hand in the direction of increasing centroid, and so the rubber also could not excite the lower normal modes. Although it was approximately the correct size and shape to excite the fundamental, it was perhaps too flimsy and lightweight to do so effectively. The foam rubber fist was taken as an extreme example of an object that is large enough, sturdy enough, and the correct shape to excite the fundamental. It produced a timbre quite similar to, and even slightly lower than the bass stroke. Due to its large size it was incapable of producing any sound aside from this.
Using insights gleaned from the foregoing study, a number of prototype striking mechanisms were built. Notable amongst them was a fully lifelike silicone rubber hand, made by alginate casting a human hand. The result was a copy accurate down to the level of detail of the fingerprints. This prototype produced a satisfying range of sounds, however it also had a few problems. It was too heavy to be actuated by practical means; the slap was not quite crisp enough at low amplitudes; and it was somewhat too floppy and in certain scenarios the fingertips would jiggle and bounce on and off the head making several onsets when only one was intended. So Kiki's final hand, whose construction is depicted in Figure 14 was made to address these issues.
The entire hand is made upon an aluminium rod, which serves as its `forearm', and which extends several inches into the hand. At the very interior of the hand, two gracile but very rigid lengths of spring steel transect the aluminium rod, which serve to make the `palm' very rigid and inflexible, thereby improving the bass stroke. The steel cross-pieces were then embedded into a piece of black vinyl sheet-rubber that had been cut roughly into the shape of a human hand, but somewhat smaller than the desired final hand size. This vinyl is less floppy than silicone, and prevents the `fingers' from bouncing on the drumhead. A small mold was then built that was somewhat larger in all dimensions than the vinyl cutout, and this was used to encase the vinyl in silicone. This gives the hand enough weight and softness to play the bass and tone strokes. Additionally, a small metal anchor was embedded in the silicone such that a wire loop protruded from the top of the hand near the `fingertips'. Attaching a cable to this loop allows the fingers to be hyperextended, effectively controlling the rigidity of the hand. In the final robot, this mechanism was under-actuated, so that that the `fingers' become more hyperextended as the arm extends. The silicone was dipped into liquid latex rubber, which cured and formed a thin skin around the entire hand. Latex has a somewhat harder surface texture than silicone, which improves the slap sound. Finally, the latex was coated with chalk dust to remove the tack from its surface texture.
This hand was not evaluated using the computational methods outlined in the foregoing study. A more complete method of comparing the robot's sound to a human's sound (an extension of the foregoing method) shall be presented in Chapter 5 below, and timbral analysis shall be presented there. However, a more qualitative study was done to assess Kiki's use of timbre. Several participants with at least some musical training, several with advanced degrees in music, listened to Kiki playing a one minute pre-programmed excerpt of music. The participants were then asked a variety of questions about timbre generally, to prime them to think critically about the role of timbre in music. Then they were asked "Do you have any remarks about Kiki's use of timbre?" Several participants gave confirming answers (perhaps suspiciously so). One said "It is pretty remarkable that it wasn't as `robotic' as I expected; not just the rhythmic pattern but the actual timbre itself. There was a lot of variation that didn't seem like it could be produced by a robot." Others said "For what is available with the djembe, given the djembe's sonic morphology, Kiki seems to make full use of timbral possibilities" and "it doesn't sound like it lacks variety in timbre ... it basically explores the whole realm." Others were more critical. Two participants, both claiming percussion as a primary instrument, thought that Kiki was better at producing bass stroke than slap. One said "When its hitting the bass note ... it sounds like a human hand; like the palm of the human hand maybe hitting it. But then it's maybe not applying as much pressure as personally I would have when I am trying to get a `thwack', when you're using these two fingers, and kind of almost doing a rim shot with the knuckle of your middle and ring finger. I would personally literally push the skin down on the djembe and thwack it with these two fingers. It gets a real snap, pop to it." The other said "I feel like a lot of the timbre comes from - especially hitting it here [on the very edge of drum] - comes from the slight curvature of your fingers ... but as far as this one goes, for the center, I think that is dead-on." The author of this dissertation agrees; this hand does not produce as satisfying a slap as some other prototypes made of harder rubber like vinyl or nitrile rubber sheet. Some participants noticed Kiki's inability to produce muted strokes and extended techniques. One said that Kiki's playing "sounds a little one-handed ... compared to a [human] player who might for example keep a hand on the drum or keep the overtones from ringing out by using a second hand." Another participant cited a skilled djembe-playing friend who will rub a finger on the head to produce a growling sound, or tap with one hand while muting different locations with the other hand. A final participant focused on Kiki's auxiliary beaters. He noticed that they produce different pitches owing to fluctuations in tension around the djembe's head. The same participant thought it would be interesting to add more auxiliary instruments such as the shaker and double-bell used ubiquitously in West African music (Kiki has a single-bell somewhat unlike those used in Africa). No participant commented on the noise of Kiki's servos. Taken as a whole, these comments seem to indicate that Kiki's sensitivity to timbre is satisfying but not indistinguishable from a human. The comments contain very clear advice about how Kiki could be improved in the future.
A synthetic hand, even a very good one, does not, by itself, guarantee a satisfying range of timbres; it must also be driven into the drum in an appropriate variety of ways.
Initially, it may seem that an arm for this purpose would need two degrees of freedom: one to control the radial distance of the hand from the center of the drum, and another roughly analogous to the flexion and extension of the human elbow, in order to strike the drum. However, informal experimentation with natural and synthetic hands revealed that different timbres can be also produced by striking the drum at different angles, which necessitates a third degree of freedom. In particular, during the tone stroke, the wrist lies approximately on (or slightly below) the plane of the drum head at the moment of impact, but for slap, the wrist is considerably below it. For bass the wrist obviously must be above the plane of the drum. These informal findings are confirmed by scrutinizing a video of djembefola Mamady Keita, as seen in Figure 15. His hand, in addition to being less rigid during slap, strikes the drum from a lower angle.
In practice, these degrees of freedom will not be entirely orthogonal, as a stroke will involve raising the synthetic hand above the drum by flexing the `elbow', which changes the angle and radial distance of the end effector from the center of the drum as well. For the sake of the present analysis, however, an orthogonal system will be imposed. The degrees of freedom under consideration will thus be the radial distance ∆x, the height ∆y of the end effector above the drum head, and the angle α of the hand with respect to the plane of the drum head.
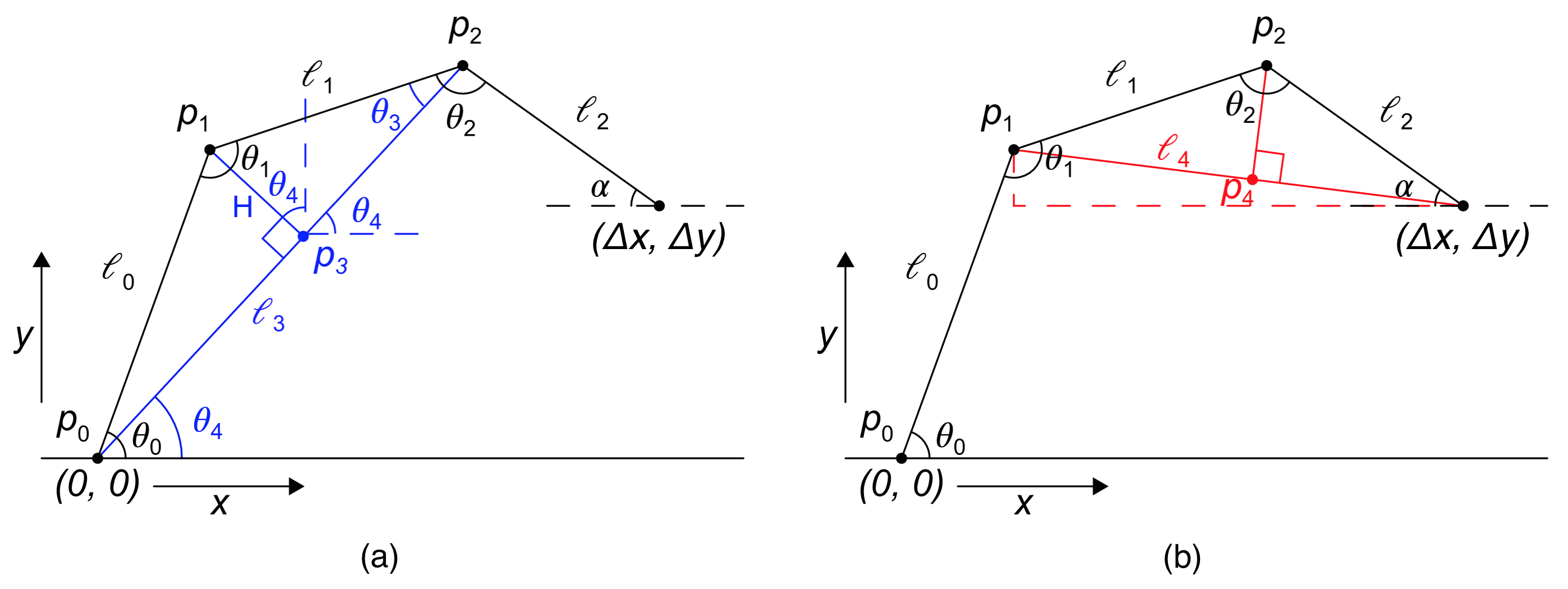
Although the inverse kinematics for three segment arms is known, the specific case in question is presented here to facilitate repeatability. Given the desired coordinates (∆x, ∆y) of the arm's endpoint and the angle α that the last segment makes with respect to the plane of the drum head, we wish to know the appropriate angle of each servo, θ0, θ1, θ2 (refer to Figure 16 for the variable names used in the following analysis) 6. To find these, it is first necessary to calculate the two dimensional position, p0, p1, p2 , of each servo. The coordinate system shall be defined such that p0 lies at (0, 0). Since the length of each arm segment, l0, l1, l2 , is constant, the position of p2 is easy to calculate.
|
p0 = (∆x − l2 cos α, ∆y + l2 sin α) |
| (4) |
Calculating the position of p
1 is somewhat more involved. First, the distance
l3 between p
0 and p
2 must be calculated (As depicted in blue in
Figure 16 (a)).
Here, the subsubscripts x and y indicate the x and y coordinates of the point. Note that a solution to the inverse kinematics will exist if, and only if
l3 ≤
l0 +
l1.
Given that, the position of p
1 is found as follows. There exists a point p
3 that lies upon
l3 and is the shortest distance, H, from p
1. The precise location of p
3 along
l3 depends upon the relative lengths, λ, of
l0 and
l1 (given here without proof).
|
λ = 0.5 + |
l02 − l12
2l32
|
; p3 = (λp2x, λp2y) |
| (6) |
The length of H is found by first finding the angle θ
3 between
l1 and
l3, using the Law of Cosines:
|
θ3 = arccos |
l12 + l32 +l02
2l1l3
|
|
| (7) |
This allows H to be found using the definition of sine.
However, on modern computers, trigonometric functions are typically implemented using successive approximation (i.e. Taylor series) and consequently have a high time complexity. Timing is highly important in musical applications, so it is therefore desirable to simplify trigonometric expressions where possible. Since sin(arccos(θ)) = √{1−θ
2}, Equation
3.7 and Equation
3.8 may be simplified as follows.
|
θ3 ′ = |
l12 + l32 +l02
2l1l3
|
; H = l1 * |
√
|
1−θ3 ′2
|
|
| (9) |
Here, the prime indicates that θ is no longer a valid angle, just an intermediate result. H is at some angle θ
4 with respect to vertical, which must be found in order to separate H into its components. Because H is perpendicular to
l3 , θ
4 is also the angle θ
4 which
l3 makes with the horizon. This angle can be found using the definition of cos, but since arccosθ is only defined for 0 < = θ < π, angles on the interval −π < = θ < 0 must be deduced manually, according to the position of p
2y.
This allows the calculation of p
1.
|
p1 = (p3x − H sinθ4, p3y + H cosθ4) |
| (11) |
Again, these trigonometric functions can be simplified, allowing the calculation of p
1 as follows.
|
θ4 ′ = |
p2x
l3
|
; p1y = p3y + H θ4 ′ |
| (12) |
There are, in fact, two solutions for the position of p
1. The other is the reflection of p
1 about
l3, and can be solved by using −H in place of H. The solution given here, chosen arbitrarily, puts p
1 farther from the body of the drum during normal operation. The angles θ
1, and θ
2 shall be calculated using the Law of Cosines, which means that, in addition to
l3, the length
l4 of the third side of triangle
l1,
l2 will need to be known (as depicted in red in
Figure 16 (b))).
|
l4 = |
√
|
(∆x−p1x)2 + (∆y−p1y)2
|
|
| (14) |
Furthermore, in order to find whether −π < = θ
2 < 0, it will be necessary to determine whether p
2 lies above or below
l4. This may be accomplished by defining the point on
l4 which lies nearest to p
2. This may be found analogously to Equation
3.6.
|
λ′ = 0.5 + |
l12 − l22
2l42
|
; p4y = λ′(∆y − p1y) |
| (15) |
The x coordinate of p
4 is not needed. It is now possible to calculate the sought angles θ
0, θ
1, and θ
2, using the Law of Cosines and the definition of cosine, again manually correcting for negative angles.
|
θ1 = arccos |
l02 + l12 − l32
2 l0 l1
|
|
| (17) |
These are the sought angles.
An optimal striking algorithm for the arm remains an open area for future study. The idea is to use a closed-loop controller to bring the hand in contact with the drum at the correct location and time and with the correct velocity, and to do so by moving along a path that can be easily interpreted visually by human interactors. The current solution implemented in Kiki involves some simplifying assumptions and heuristics, and works acceptably well provided that there is not a great change in velocity between adjacent strokes. More information on this algorithm is presented in Chapter 5. Further research is also needed to more rigorously assess the degree to which this robot achieves its stated purpose, i.e. how perceptually similar its timbres are to a human player. This latter point is somewhat complicated and is also treated to a certain extent in Chapter 5.
Footnotes:
6The algorithm described in this section is given in pseudocode in
Appendix A