The last movement of Arnold Schönberg's Fünf Klavierstücke, Opus 23 (1923) is the first piece in which he employs his 'Method of Composing with Twelve Tones Which are Related Only with One Another'. 1, 2 As such, the compositional ideas therein are often considered to represent a pioneering departure from the conventions of the time. A scrupulous examination of the various compositional techniques used therein, however, reveals that many of the 'groundbreaking' techniques were already present in the work of other composers, most notably Charles Ives and Josef Hauer. The music of Opus 23, therefore can be seen not as a crisp departure from established techniques, but rather as a culmination of nascent techniques.

The features of Op. 23 #5 that set it apart from Schönberg's previous works are that it is both serial, and dodecaphonic. These terms are often confused,3 so I shall clarify the definitions that I will use throughout this paper here. By serial, I mean that some element of the music (in this case the pitches) is put into a series, or ordered collection, which is then used in a significant structural manner within the piece. By dodecaphonic I mean a musical texture in which the 12 pitch classes are used with roughly statistical equivalence in the aim of annihilating a sense of 'tonic'. Schönberg's own description of his "Method of Composing with Twelve Tones Which are Related Only with One Another", which is used first in Op.23 #5, confirms that his technique is both serial and dodecaphonic. Of this, he says:

The method consists primarily of the constant and exclusive use of a set of twelve different tones. This means, of course, that no tone is repeated within the series and that it uses all twelve tones of the chromatic scale...4

This clearly states that his method comprises the combination of dodecaphony ("all twelve tones"), and serialism (he refers to "series" explicitly).

These principals are seen quite clearly in Op. 23 #5, which opens with the following melody in the right hand:

This melody is indeed dodecaphonic, as it contains every pitch-class exactly once. The piece is, furthermore, serial, because the entire piece is composed by the successive repetition of these pitch-classes in this order, without even any of the permutations (transposition, retrograde, inversion) that may be expected by one who is familiar with Schönberg's later works.

Although the extensive use of these serialism and dodecaphony was new for Schönberg in Op. 23 #5, both ideas had previously existed. The idea of a series as the basis for composition is at least as old as the isorhythmic motets of the late 14th and early 15th centuries. John Dunstable's 'Veni Sancte Spiritus / Veni Creator Spiritus' is a good example. In this piece, both pitch and duration are serialized in the tenor part. The structure of the entire work is based upon this 22 note pitch-series:

which is executed thrice, and this 11 note duration series:

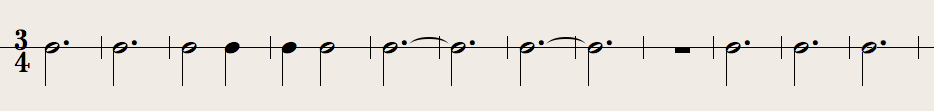
which is executed 6 times in various temporal permutations over the course of the work.

Dodecaphony, likewise, was a favorite technique of Mozart. This remarkable and famous passage from the fourth movement of his Symphony 40 in G minor contains a succession of every pitch-class except the tonic (pitch-class numbers have been given for clarity):

Here, it seems relatively clear that he is using eleven pitches to undermine the twelfth. Another example occurs in the third movement of his Symphony 41 in C major, where several overlapping statements of a rather chromatic theme results in this:

which contains every pitch-class in the space of 6 short beats (pc numbers are shewn in red). Taken out of context, these measures have no identifiable key. This appears to be a deliberate attempt to subvert the tonic. One may fancy that this is the result Mozart's characteristically humorous and defiant attitude towards composition. Two measures later, when he works his way out of this dodecaphonic mess, he ends the passage on a deceptive cadence, which further gives the sense that he is consciously sabotaging the tonic.

Although both serialism and dodecaphony were centuries old by 1923, the systematic combination of the two appears to be much newer. In 1922, Josef Hauer published an article called "Sphaerenmusik" in which he says:

We have twelve tempered halfsteps ("solar systems") with a calculated 479,001,600 melodic possibilities ("star paths"). Within the twelve tones none may be repeated or excluded--this is self-evident. Identical tones must be distanced from one another as far as possible.5

This is notably similar to Schönberg's later description of his own technique, as cited above. Clearly, dodecaphony is suggested in the idea of neither repeating nor excluding tones. Serialism is suggested because the only way to literally distance the pitches as far (in pitch space) from one another as possible is to serialize their order. Furthermore, 479,001,600 is precisely 12 nPr 12, or the number of ordered collections that can be derived by taking members of a 12 member set 12 at a time (i.e. the number of possible tone-rows).

Schönberg read this article around the time it was published. Later, in December of 1923, shortly after he wrote Op. 23, he indicated in a letter to Hauer that he was aware of the similarity of technique. He said:

...about 1 1/2 or 2 years ago I saw from one of your publications that you were trying to do something similar to me, in a similar way. After coming to terms with the painful feeling that someone else, by also being engaged in something I had been thinking for pretty well 15 years, was jeopardizing my reputation for originality...6

A decade later, in his 1934 lecture 'Composition with 12 Tones', Schönberg appears to retrospectively claim that he proposed the idea of combining serialism and dodecaphony even before Hauer, as early as 1911. He said:

"Why such a set should consist of twelve different tones, why none of these tones should be repeated too soon... Discussing such problems in my Harmonielehre..."7

These problems, however, do not appear to be discussed explicitly in his 1911 treatise Harmonielehre.

In any event, a discussion of originality between these two men seems rather unavailing in light of the fact that decades before this correspondence, in 1901, Charles Ives was already using both dodecaphony and a highly idiosyncratic type of serialism together in his piece 'From the Steeples and the Mountains'. In measure 17 of this work, a cannon begins between the Trumpet, dux, and the Trombone, comes. The texture is clearly dodecaphonic. The first thirteen notes of the dux contain the entire twelve note aggregate, with only the F♮ repeated:

Similarly, the next 11 notes in the dux contain every pitch-class except E♮. This continual cycling of all of the pitch classes of the aggregate meets the condition for dodecaphony, and it is even more frequent when the dux is taken together with the comes. Starting at measure 13, for instance, with both voices together, the aggregate is completed in only three and a quarter measures, as opposed to the five measures it took for the dux alone:

So, in the first eight measures of the cannon every pitch is heard exactly 4 times, excepting F and D which are heard 5 times each, and E and C♯, which are heard only thrice each. One may argue that this is not strictly dodecaphonic, because the pitch classes do not occur with precise statistical equivalence. The same, however, is true of Schönberg's Op. 23 # 5. At the end, for instance, he makes his cadence with incomplete segments of the row:8

Here, order numbers for the row are shewn in different colors to separate repetitions of the row. The green numbers correspond to the previous, complete statement of the row (the rest of the row is not shewn). The blue numbers correspond to the penultimate statement of the row, which lacks the last four elements. The last statement of the row lacks also lacks the last four elements, and additionally lacks the sixth, as indicated by the red numbers. In other words, if we can call Op 23 #5 'dodecaphonic', even with its minor statistic imperfections, then we may also call Ives 'dodecaphonic'.

Not only is 'From the Steeples and the Mountains' dodecaphonic, it is also serial. Firstly, any canon in rounds, like this one, depends on the serialization of pitches, because the comes repeats the exact same pitches (or some permutation of them) as the dux in the exact same order. Here, the pitch series is not repeated literally, but rather it is transposed, a concept which Schönberg did not make use of until his Op. 25. Furthermore, this is essentially a crab-cannon, which means that after the midpoint of the piece, the series is executed in retrograde, a concept that took Schönberg even longer to develop. What makes Ives' retrograde idiosyncratic, however, is that it is not the strict pitches-series, but rather the series of measures themselves that are performed in retrograde. For instance, measures 14 and 15, as shown above, become measures 35 and 36 in retrograde, like so:

The content of measure 14 is identical to the content of measure 36, likewise is 15 to 35. The only difference is that the order of the measures has been reversed. In other words, these measures have been treated as an ordered collection, and the resultant series has been abstracted to the extent that a regular permutation (i.e. retrograde) can be applied to it in a unique and thoughtful way.

It should be mentioned that this piece could not have had any direct influence on Schönberg in 1923, because it was neither performed nor published until 1965 (the extremely low church bells make its performance impractical).9 It is not, of course, my stated purpose to show what influenced Schönberg, but only to show which of his techniques were already in use. In any event, the fact of 'From the Steeples and the Mountains' perhaps suggests that there existed a sort of zeitgeist that promoted these techniques.

---

Not only had the general concept of combining serialism and dodecaphony already been put into practice by 1923, but many of the more specific ways that this combination is carried out in Op. 23 #5 were also already in use, most notably by Josef Hauer. Here I will point out a few passages where the similarities are most apparent.

In places, Schönberg's pitch-series is paired with a durational series in much the same way that Dunstable's color is paired with his talea in the aforementioned motet, albeit on a much more momentary scale. In other words, a pitch series containing a certain number of elements (in this case twelve) is repeated several times and superimposed over a duration-series with a different number of elements that is also repeated several times. A good clear example of this may be seen starting in measure 70:10

Here, the basic duration-series:

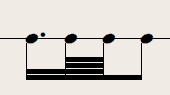
is repeated about 5 times, while the pitch series is repeated twice, as indicated by the red order-numbers. Additionally, registration plays an important role in the musical growth of this passage. At the beginning of this passage each individual element of the pitch series is paired with exactly one element of the rhythmic series. In measure 72, Schönberg creates musical growth, and makes the music increasingly 'heavy' by introducing two pitch elements per rhythmic element. This heaviness is further accentuated by the drastic shift in registration between measures 71 and 72.

Josef Hauer also pairs a dodecaphonic pitch-series and a different-length durational-series in the first measures of his 1909 piano piece 'Nomos', Op. 19. The first 15 measures of the right hand are shown here (in the score, the left hand follows the right in octaves):

Starting in measure 1, he pairs a pitch series of twelve elements (one for every pitch in the aggregate) with a duration series of 5 elements:

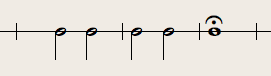
The process that is started in these fifteen measures continues for thirty-six measures total, until the duration series comes back into phase with the pitch series so that the last note of one corresponds to the last note of the other. One may correctly predict that this process will require n number of pitch or durational elements to come to completion, where n is the least common multiple of five (the number of durational elements) and twelve (the number of pitch elements), or sixty elements total. This is just enough elements for five statements of the pitch series and twelve statements of the rhythmic series. Although this menas that Hauer never uses more than one pitch element per rhythmic element (as Schönberg does), he does, like Schönberg, use careful registration to control the growth of the music. In the measures reproduced above, there is a clear overall ascending trend to the melodic line. This trend continues through the first 7 statements of the rhythmic series, at which point the trend is reversed and the music descends back to the opening register over the next 5 statements. This careful use of register gives the music a sort of dramatic arch.

A completely different passage where Schönberg uses a rhythmic and textural musical structure reminiscent of Hauer occurs at the passage starting in measure 44 of Op. 23 no 5. Here, there is a four-voice texture, and the composite rhythm contains one attack per eight-note. Each successive attack contains the next pitch of the series, and each voice holds its previous pitch until the next attack in that voice:11

One may imagine a similar, slightly more didactic musical texture in which the pitches in the series are assigned to the voices in a round-robin fashion. In such a texture each note would have a duration of four eighth notes, and the first voice would receive the the first, fifth, and ninth pitches, the second voice would the second, sixth and tenth, and so forth. Schönberg's approach, however, is much more artistic than this, and again as in the previous example, registration plays an important role in his approach. The first evidence that his distribution of pitches is primarily registral is that there are no voice crossings in the entire passage. Furthermore, each individual voice is relatively conjunct. Of the 33 melodic intervals in this passage, 14 of them are minor seconds, five of them are major seconds. Larger intervals are progressively less frequent, and there is no interval greater than a minor sixth. This interval structure is enumerated in the following table:

melodic interval	number of occurrences
m2	14
M2	5
m3	4
M3	3
P4	2
TT	3
P5	1
m6	1

The high incidence of small intervals is remarkable, considering the disjunct nature of the piece as a whole, and seems to be the result of a conscious attempt to control the register of each voice.

A very similar technique is a favorite of Hauer's. He calls this type of musical texture a 'continuum'.12 A passage passage where he employs it occurs in his Violinkonzert, Op. 54, starting at measure 9:13

In this passage, the pitches of a dodecaphonic series are distributed amongst four voices in such a manner that each voice stays within the range of a minor third. This is the narrowest possible distribution of twelve pitch-classes over four voices. Here registration is the only factor in determining the distribution of pitches amongst the voices. Simon Shaw-Miller explains Hauer's use of 'continuum' in detail, and provides the following illustration:14

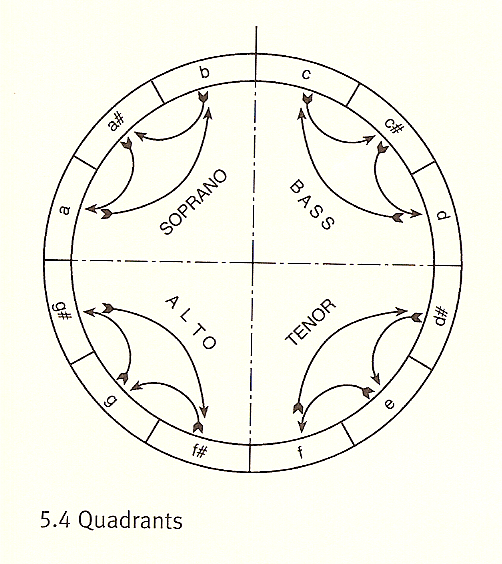
which clarifies Hauer's approach. Notice that although the this is very similar to the passage from Schönberg, there are also some important differences: Hauer uses 'continuum' to explore the musical structure that is inherent in his pitch series, while Schönberg appears to be using the registeration of pitches within the row for expressive purposes. Specifically, he seems to be trying to control the trajectory of each voice, so that the uppermost voice basically takes an ascending trajectory, while the lowest voice basically takes a descending one, and the inner voices are registrated such that they can be easily reached by the pianist's hands, given the trajectory of the outer voices. The generally opposite trajectory of the outer voices creates an expressive musical tension.

Examining the order-numbers provided in the above excerpt from Hauer's Op. 54 reveals that the aggregate is not expressed in exactly the same order every time. John Covach explains that Hauer systematically rearranges the order of the pitch-classes within each discrete trichord between each statement of the aggregate. More importantly, once the trichordal orderings have been exhausted, he rotates each hexachord, so that the first pitch in each hexachord becomes the second, the second the third, etc... and the last becomes the first. Covach clarifies how the rotation works with the following diagram in which the pitch-class numbers of the first and third row form in the piece have been aligned to illustrate the rotational relationship15:

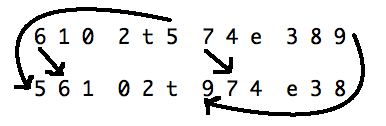
This system illustrates two more compositional techniques that are used in the works of Hauer prior to their use in Op. 23 #5. The first is the principal of rotation, and the other is the use of the hexachord as a basic compositional unit. As for hexachords, Hauer's theory is relatively complex. In his aforementioned 1922 article, he first states that "A good atonal composition" should be constructed by "dividing them [the twelve tones] into two groups of six tones each." He then explains that he has invented compositional structures called 'tropes' that use these hexachords as the basic unit, and states that he has already written each one down. Later, in his 1925 book Vom melos zur pauke, he provides a table that helps to clarify that a 'trope' is a complimentary pair of unordered hexachords. He gives 44 of them: one corresponding to each of Forte's 35 hexachord classes, as well as one for each inversion of each of Forte's hexachord classes whenever the inversion produces a distinct normal-form. For example, the first trope comprises the hexachord {0, 1, 2, 3, 4, 5} (which is Forte's hexachord-class 6-1), and its compliment {6, 7, 8, 9, T, E}.

Schönberg also identifies the hexachord as a basic compositional unit in Op 23 # 5. His row, as presented above is thus:

1 9 E 7 8 6 T 2 4 3 0 5

Each discrete hexachord of this row is a member of class {0 1 2 3 5 7}, where the second hexachord is inversionally related (specifically I eleven) to the first.16 This row, then has an identical structure as Hauer's 9th trope which he (Hauer) illustrates with the following diagram17:

Here the pitch-classes of one hexachord are connected by orange lines, and the other by blue ones. This makes the inversional relationship of the hexachords clear, as the illustration is bilaterally symmetrical about the ordinate axis. The principal of hexachordal combinatoriality is inherent in this symmetrical structure. It is easy to visualize that flipping the image about the ordiante axis results in each hexichord mapping to its compilment, which is analogous to paring a P-naught and I-eleven in a combinitorial fashion. Although these properties are not exploited by Schönberg in Opus 25, the hexachordal structure seems deliberate (especially in light of his later works), and indicates that Schönberg was, like Hauer, thinking of the hexachord as a basic structural unit in Op 23 #5.

Regarding rotation, the theorist Walter Szmolyan demonstrates that Hauer first employed it systematically in his 1922 "Etuden fur Klavier" Op. 2218. It may be further noted that the concept of rotation is implicit in the above example from Opus 19. There, although it is perhaps somewhat trivial, each statement of the duration-series begins with the pitch-series rotated 5 members to the left. Anyhow, Szmolyan distinguishes two types of rotation in Hauer's music. The first, which he calls "kline Abwandlung" respects hexachordal partitioning. The aforementioned example from Op. 54 is an example of this type of rotation. The other type of rotation, "grosse Abwandlung", is a rotation of the entire row, irrespective of hexachordal boundaries. In this type of rotation, the first element of the series may become the second, the second the third ... the seventh the eighth, and the 12th the first.

It is this latter type of rotation, "grosse Abwandlung", of which Schönberg makes use in his Op. 23 #5. A clear example of this technique is in the opening measures:19

Here the right hand plays the row in its original form (order numbers are shewn in red), while the left hand also plays it, but starting on the 6th element (with order numbers in blue). In other words, the left-hand row has been derived from the right-hand row by rotating it five elements to the left, like so:

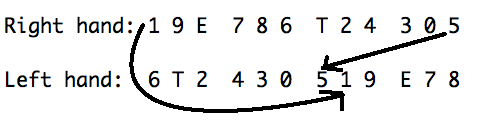
The implementation of the rotation here differs from Hauer's in that Hauer only used different rotations of the series successively, while here Schönberg is using them simultaneously. Nonetheless, on a theoretical level (i.e. on the next abstract level below individual implementation), the usage is identical.

In summary, it has been shewn that many of the techniques of Schönberg's Op. 23 #5 were already present in the works of other composers. The ideas of serialism and dodecaphony were each centuries old. The idea of combining serialism and dodecaphony was decades old and had been employed creatively by Charles Ives as early as 1901. Other more specific techniques, like hexachordal partitioning, set rotation, 'continuum' and others had been employed by Josef Hauer in the preceding years. What makes Schönberg's work special, therefore, is not any specific revolutionary compositional technique, but rather the high level of skill with which he combined and used those techniques.

1. "The first works in which Schoenberg deliberately applied tone rows were the five piano pieces Op. 23, of which, however, only the last has a complete row of twelve tones." Grout and Palisca, A History of Western Music, 716.
2. "Schoenberg first used the twelve-tone system in in Five Piano Pieces, Op. 23..." Wink and Williams. Invitation to Listening, Second Edition. Boston, Houghton Mifflin, 1976. p340.
3. My dictionary, for instance, gives the definition of dodecaphony sub verbo 'serialism': "a compositional technique in which ... the twelve notes of the chromatic scale are used to generate the harmonic and melodic basis of a piece... See also twelve-tone". Dictonary.app, Version 2.0.3 (51.5), s.v. 'serialism'. (Cupertino: Apple Computer Inc, 2005-2007).
4. This is from his 1941 lecture "Composition with 12 Tones". Arnold Schoenberg. Style and Idea Ed. Leo Stein. Trans. Leo Black. Berkeley: University of California Press, 1975, pp. 214-26. Due to the limited resources of our library, this quote was taken from a partial reprint in Oliver Strunk. Source Readings in Music History, Sixth Edition. Ed. Leo Treitler. New York: W W Norton & Company, 1998, p 1359.
5. Hauer, Josef. "Sphaerenmusik". Melos. Volume 3, 1922. pp. 132-133. This translation is taken from: John Covach. Music and Theories of Josef Mathias Hauer. Ph.D. Dissertation, University of Michigan, 1990. p. 155.
6. Arnold Schoenberg, Arnold Schoenberg Letters, 103.
7. Oliver Strunk, Source Readings in Music History, p 1359.
8. Mechanically reproduced from Arnold Schönberg, Fünf Klavierstücke, 19.
9. "from the steeples and the Mountains was composed in 1901 and first performed in 1965, after Ives's [sic] death."Brennan and Clarge, Who's Who of the Pulitzer Prize Winners, 421.
10. No Note.
11. Mechanically reproduced from Arnold Schönberg, Fünf Klavierstücke, 18.
12. Hauer's theory of the 'continuum' is explained in detail in: Simon Shaw-Miller, Visible Deeds of Music, 167.
13. When I wrote this, I mistakenly thought that Op. 54 was from early 1923, but now that I am double checking my bibliography... it turns out that it is actually from 1928. This however, does not totally floccinaucinihilipilificates my argument in this paragraph. Hauer was used dodecaphonic continua in earlier examples. A nearly identical three-voice example is in Op. 20/7, mm. 1-8, composed between 1920 and 1922. In any event, I will let this section stand as an interesting comparison of style.
14. Simon Shaw-Miller, Visible Deeds of Music, 169.
15. John Covach, Music and Theories of Josef Mathias Hauer, p.175.
16. Krzyzaniak, Michael. Atonal Calculator.
    http://orpheansculptures.com/AtonalCalculator/. Internet: accessed November 28, 2010.
17. Josef Hauer. Vom Wesen des Musikalischen. From a fold-out on the last, unnumbered page.
18. Szmolyan, Walter. "Eine Violinkonzert vom J. M. Hauer". Oesterreichische Musikzeitschrift. 24/10 (1969): 578-583. Taken from: John Covach, Music and Theories of Josef Mathias Hauer, 171. Covach says "Sengstschmid has determied that Hauer was utilizing systematic rotation techniques as early as his Etuden Fur Klavier, Op. 22 (1922-23)".

• Elizabeth A. Brennan, Elizabeth C. Clarage Who's Who of the Pulitzer Prize Winnersp421 Covach, John. Josef Matthias Hauer. www.ibiblio.org/johncovach/hauerbio.htm. Internet: Accessed November 28, 2010.
• Covach, John. Music and Theories of Josef Mathias Hauer. Ph.D. Dissertation, University of Michigan, 1990.
• Forte, Allen. The Structure of Atonal Music. New Haven: Yale University Press, 1977.
• Grout, Donald and Palisca, Claude. A History of Western Music, Sixth Edition. New York, WW. Norton & Company, 2001.
• Hauer, Josef. Nomos, Op. 19. Wien: Verlag Doblinger, 1976.
• Hauer, Josef. "Sphaerenmusik". Melos, 3(1922):132-133.
• Hauer, Josef. Violinkonzert, Op. 54. Wien: Universal-Edition, 1977.
• Hauer, Josef. Vom Melos zur Pauke. Wien: Universal-Edition, 1967.
• Hauer, Josef. Vom Wesen des Musikalischen. Berlin-Lichterfelde: Robert Lienau, 1966.
• Ives, Charles E. From the Steeples and the Mountains. New York: Peermusic Classical, 1965.
• New Grove Dictionary of Music and Musicians, s.v. "Twelve-note composition", by Paul Lansky and George Perl. Edited by Stanley Sadie and John Tyrell. London: MacMillian Publishers, 2001.
• Plebe, Armando. La dodecafonia. Bari: Editori Laterza, 1962.
• Schönberg, Arnold. Arnold Schoenberg Letters. Edited by Erwin Stein. Translated by Eithne Wilkins and Ernst Kaiser. London: Faber and Faber, 1964.
• Schönberg, Arnold. Ausgwahlte Briefe. Mainz: B. Schott's Söhnne, 1958.
• Schönberg, Arnold. Fünf Klavierstücke, Op. 23. Copenhagen: Wilhelm Hansen Edition, 1923.
• Schönberg, Arnold. Style and Idea. Edited by Leonard Stein. Translated by Leo Black. Berkeley: University of California Press, 1975.
• Schönberg, Arnold. Suite Für Klavier, Op. 25. Wien: Universal Edition, 1925.
• Schönberg, Arnold. Theory of Harmony. Translated by Roy E. Carter. Berkeley: University of California Press, 1978.
• Straus, Joseph N. Introduction to Post-Tonal Theory. New Jersey: Prentice Hall, 1990.
• Strunk, Oliver. Source Readings in Music History, Sixth Edition. Edited by Leo Treitler. New York: W W Norton & Company, 1998.
• Shaw-Miller, Simon. Visible Deeds of Music. New Haven: Yale University Press, 2002.
• Szmolyan, Walter. "Eine Violinkonzert vom J. M. Hauer". Oesterreichische Musikzeitschrift. 24/10 (1969): 578-583.
• Wink, Richard and Williams, Lois. Invitation to Listening, Second Edition. Boston, Houghton Mifflin, 1976.